parallelogramm im Rechteck

Question

Ich habe ein Problem mit einer ähnlichen Aufgabe,die hier schon mal bearbeitet wurde: https://www.mathelounge.de/354622/quadratische-funktion-rechteck-parallelogramm-einbeschrieben

Ich brauche jedoch eine allgemeine Formel für ein allgemeines Parallelogramm und scheitere die ganze Zeit daran,dass ich in meiner Zielgleichung zwei Unbekannte,statt einer habe. Ich sitze schon den zweiten Tag dran und kriege es nicht hin,die eine Variable zu entfernen!

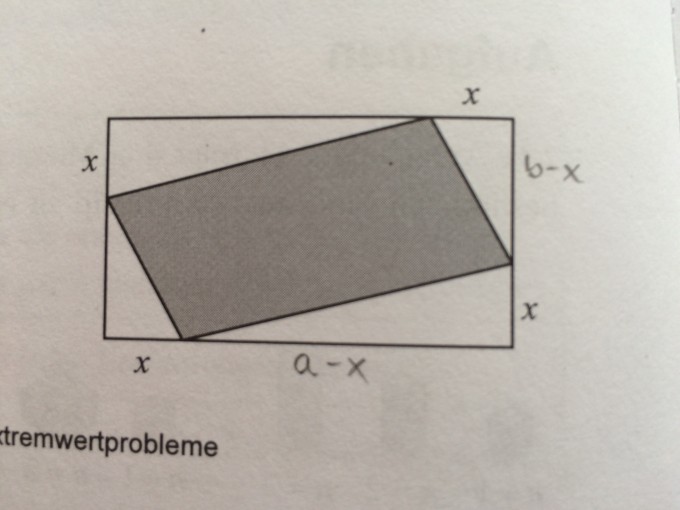
Hier also die Aufgabenstellung:   Auf den Seiten eines Rechtecks wird die Strecke x jeweils ausgehend von den Eckpunkten entsprechend dem Umlaufsinn abgetragen. Die vier freien Endpunkte werden miteinander verbunden. Für welche Länge x wird der Flächeninhalt des Parallelogramms minimal?

Die Funktionsgleichung,die ich bis jetzt zusammengestellt habe und an der ich die ganze Zeit tüftle,sieht so aus: ab-(a+b)x+2x^2

Comments

Eine Nebenbedingung,die Ich anwenden kann wäre,dass bei einem Rechteck die Summe der beiden Seitenlängen = der halbe Umfang des Rechtecks sind.

Dann könnte ich in meiner Gleichung a+b durch 1/2U ersetzen und wäre somit diese Unbekannten los...Aber es bleibt dann immer noch ab.....

ab - 1/2Ux + 2x^2

Answer 1

A = a·b - (a - x)·x - (b - x)·x

A = 2·x^2 - x·(a + b) + a·b

A' = 4·x - a - b = 0 --> x = (a + b)/4