Komplexe Zahlen richtiger Lösungsweg Aufgabe mit z^3

Question

ich habe ein paar Fragen zu einer Aufgabe zu "Komplexen Zahlen", dafür habe ich die Aufgabe mal als Bild hochgeladen.
Mein Lösungsweg wäre folgender, zuerst das erste Paket dividieren ich komme dabei auf -3+j und dann würde ich einfach
die -2+2j abziehen. Somit hätte ich z^3= -5+3j

Kann ich das einfach so machen, weiter würde ich dann die Polarform aufstellen mit
r*e^iphy und dann durchrechnen mit k=1,2, ... n-1 um auf z0 bis z3 zu kommen.

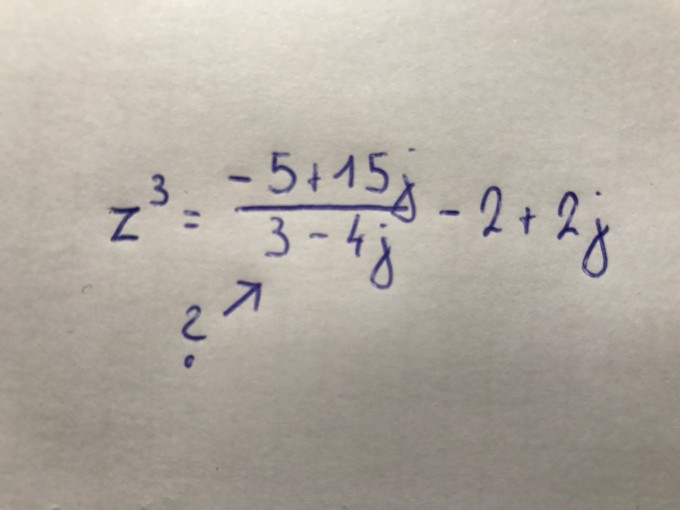
Wäre das mit diesem Beispiel so machbar und hat jemand Lust da auch mal nachzurechnen?

Comments

"Somit hätte ich z³= -5+3j"

Das ist soweit richtig.

---

für r dann ca. 5,83 und phy=149°

z0=3Wurzel5,38 * e^i(149°/3)

z1=3Wurzel5,38 * e^i(149°+360°/3)

z2=3Wurzel5,38 * e^i(149°+720°/3)

Ist das so korrekt?

---

Wird wohl sinnvoll sein, die Originalaufgabe mitzuteilen!
(vgl. die Antwort von Wolfgang!)

Answer 1

 

>  und dann würde ich einfach die -2+2j  abziehen. Somit hätte ich z³= -5+3j

 da du  -2+2i  nicht subtrahiert hast, ist das richtig.

Auch der Restplan klingt gut.

Gruß Wolfgang

Comments

warum denn hier noch ein - extra?
Ich dachte mein Ansatz wäre korrekt mit -3+j -2+2j oder habe ich was entscheidenes übersehen?

---

> oder habe ich was Entscheidendes übersehen? 

Hast du nicht.

 -3+j -2+2j =  -3+j + ( -2+2j ) , du hast also nicht "abgezogen" und das war richtig :-) 

In deinem Text steht das anders:

> und dann würde ich einfach die -2+2j abziehen. Somit hätte ich z³= -5+3j