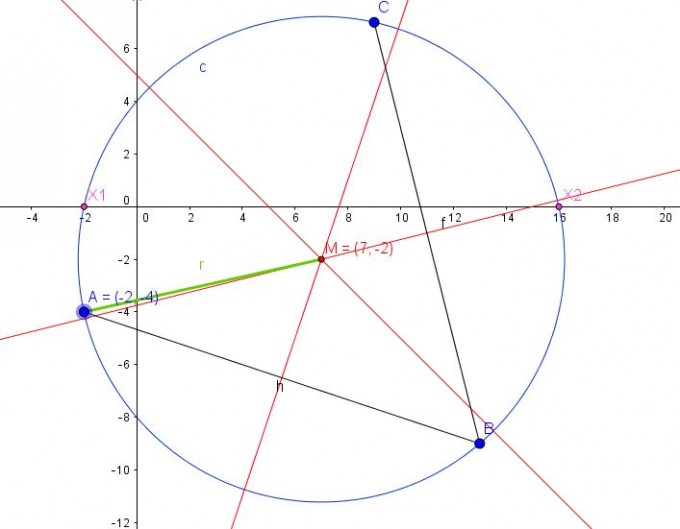
Der Schnittpunkt der Mittelsenkrechten (Streckensymmetralen) ergibt den Schnittpunkt des Kreises, auf dem alle dre Punkte liegen. Wenn du diese Symmetralen zeichnest, ist in dieser Aufgabe M mit den Koordinaten (xm|ym) = (7|-2).
Die allgemeine Form für eine Kreisgleichung lautet:
$$ k(x) = (x - x_m)^2 + (y - y_m)^2 = r^2 $$
in deinem Fall
$$ (x - 7)^2 + (y + 2)^2 = r^2 $$
r2 ermittelst du, indem du die Koordinaten von enem der drei Punkte für x und y einsetzt, ich habe Punkt A gewählt:
$$ (-2 - 7)^2 + (-4 + 2)^2 = r^2 \\81 + 4 = r^1 \\85 = r^2 $$
Die Kreisgleichung lautet also
$$ (x - 7)^2 + (y + 2)^2 = 85 $$
Die Schnittpunkte mit der x-Achse errechnene sich, indem man für y null einsetzt:
$$ (x - 7)^2 + (0 + 2)^2 = r^2 \\x^2 - 14x + 49 + 4 = 85 \\x^2 - 14x - 32 = 0$$
Die p/q-Formel ergibt
$$ x_{1,2} = 7 \pm \sqrt{49 + 32} $$
also ist
x1 = -2 und x2 = 16
Damit hast du auch die Nullstellen. Bei Fragen einfach melden.