Mathematikabitur 2014. c)Auf Erdölfeld wird Öl gefördert. 2) Fördermenge? und 3)?

Question

Wie geht man bei dieser Aufgabe c) bei 2) und 3) vor ? Wie lautet bei diesen Aufgaben der Rechenweg?

Comments

Bitte Text auch als Text eingeben: https://www.mathelounge.de/schreibregeln

Wie genau hängt das zweite Bild mit dem ersten zusammen?

---

Beim zweiten Bild steht f (x) könnte vielleicht nützlich sein

Answer 1

Bei 2) musst du das Integral von 0 bis 2 berechnen. Ergebnis = 4,389

zu 3)

f(x) = (2 - x)·e^x

f'(x) = (1 - x)·e^x

Für die Geradengleichung in der Form g(x) = mx + b brauchst du die y-Koordinate des Punktes (5/4|f(x)) und die Steigung an dieser Stelle:

$$f(\frac{5}{4}) = \frac{3}{4} · e^{\frac{5}{4}} \\f'(\frac{5}{4}) = -\frac{1}{4} · e^{\frac{5}{4}}$$

 

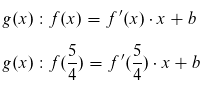
Werte einsetzen und nach b auflösen:

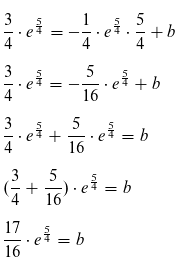
Für die Geradengleichung ergibt sich somit:

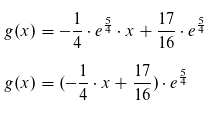
Wenn du jetzt noch 1/16 ausklammerst, kommst du auf das Kontrollergebnis.