Wie kann man diese Differentialgleichung mit Hilfe von Aufgabe 1 lösen? Aufgabe 2 y''' - 3y' + 2y = 0.

Question

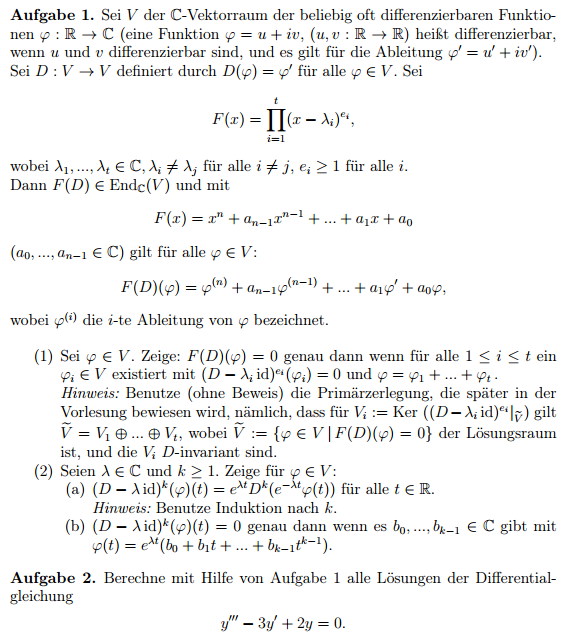
Ihr Lieben,

ich muss diese 2 Aufgaben lösen, aber ich hab doch keine Ahnung, wie ich anfangen kann.

Würde mich freuen, wenn ihr mir helfen könntet. 

Vielen Dank schonmal im Voraus. :)

LG

Wie kann man diese Differentialgleichung mit Hilfe von Aufgabe 1 lösen? Aufgabe 2 y''' - 3y' + 2y = 0.

Comments

Bei A2  hilft 

http://www.mathematik.uni-stuttgart.de/studium/infomat/HM-Rump-WS0708/Folien/folien_Nov20.pdf

Seite 2  ,  "Die homogene DGL"  

Sorry, hatte übersehen, dass du das "mit Hilfe von A1"  machen musst.

Answer 1

Zu Aufgabe 1 kannst Du in Heusers "Gewoehnliche Differentialgleichungen" den Abschnitt 15 "Die homogene lineare Differentialgleichung n-ter Ordnung" lesen.

Bei Aufgabe 2 musst Du die Dgl \(y'''-3y'+2y=0\) erstmal in die passende Form \(F(D)y=(D-1)^2(D+2)y=0\) bringen. Nach (1) haben Lösungen stets die Form \(y=y_1+y_2\) mit \((D-1)^2y_1=0\) und \((D+2)y_2=0\), und nach (2b) ist \(y_1=e^t(a_0+a_1t)\) und \(y_2=b_0e^{-2t}\).