gegeben habe ich folgende Aufgabe.
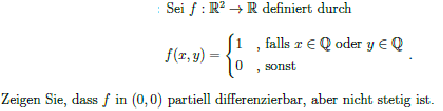
Ich habe bereits gezeigt, dass f in (0,0) partiell differenzierbar ist.
$$ \lim_{h\to0}\frac { f(h,0)-f(0,0)}{ h }$$= $$ \lim_{h\to0}\frac { 1-1}{ h }$$=$$ \lim_{h\to0}\frac { 0}{ h }$$=$$0$$
Aber wie zeige ich jetzt, dass f nicht stetig ist?
lg