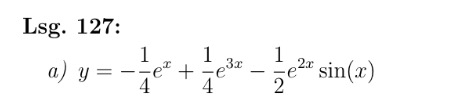Ich habe die Gleichung:
y''-4y'+3y = e^{2x}*sin(x) gegeben.
Die homogene Lösung hab ich nun berechnet:
C1*e^{3x}+C2*e^x
Und die allgemeine Lösung:
y= C1 *e^x + C2e^{3x}-1/2e^2x*sin(x)
Nun wollte ich die spezielle Lösung berechnen mit den Bedingungen y(0)=0 und y'(0)=0.
Mein Problem ist das ich es nicht schaffe C1 und C2 zu berechnen.
Hab die allgemeine mal abgeleitet und dann die Bedinungen eingesetzt, was mich aber nicht wirklich weitergebracht hat.
Denke das ich bis hierhin alles soweit richtig habe, da die Musterlösung bis auf die beiden C-Werte identisch ist.
Wäre dankbar wenn mir jemand mal schreiben könnte wie ich dadrauf nun kommen soll.
Auf dem Bild nochmal die Lösung die am ende rauskommen sollte.
mfg