Fourier-Transformation: Trapez

Question

Die Aufgabe ist die Fourier transformierte des trapezsignals zu berechnen

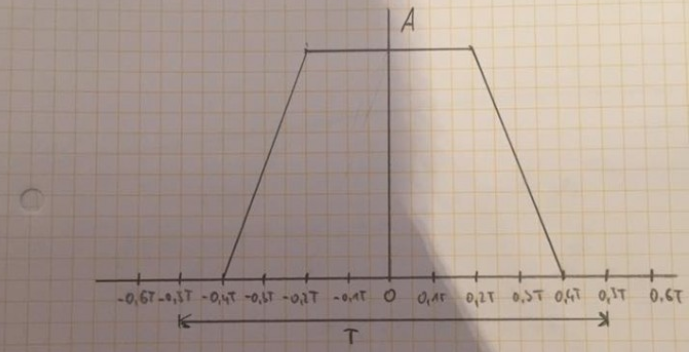
\( x(t)=\left\{\begin{array}{cc}{0} & {\text { für } \quad t \leq-0,4T} \\ {A+\left(\frac{t}{0,2T }\right) \text { für }} & {-0,4 T<t \leq-0,2\, T} \\ {A} & {\text { für }-0,2\,T<t \leq 0,2\, T} \\ {A-\left(\frac{t}{0,2\,T}\right) \text { für }} & {0,2 \,T<t \leq 0,4\,T} \\ {0} & {\text { für} \quad t>0,4}\end{array}\right\} \)

 

Comments

Hallo, wäre es möglich die komplette Fourier-Reihe aufzuschreiben?

---

Hallo,

zunächst stimmt Deine Definition von x nicht mit dem Graphen überein. Zum Beispiel wäre x(0.4*T)=A-2 und nicht 0, wie die Skizze zeigt?

Im übrigen bedeutet die Berechnung der Fourier-Koeffizienten die Berechnung eines Integrals, das zwar aufwändig ist aber im Prinzip einfach. Hast Du auch schon an die Symmetrien gedacht? Frag doch lieber, was Dir unklar ist.

Answer 1

Hi, mir ist unklar wie ich das Fourier Koeffizienten berechnen kann.

Comments

Diese beliebte Aufgabe wird bald ihren 5. Geburtstag feiern dürfen; erfreulich!

Da scheint es sich um einen einmaligen Trapez -Puls zu handeln, nicht periodisch. Daher sind auch keine Koeffizienten für eine Fourier -Reihe ermittel bar.

Dies haben wir kürzlich z. B. bei https://www.techniker-forum.de/thema/fourier-transformation-trapezimpuls.126884/ diskutiert.

Für die gesuchte Fourier -Transformierte gibt es eine Darstellung als Differenz zweier Dreieck -Pulse.