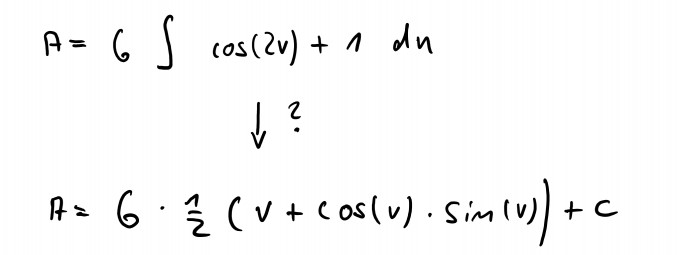Integral Ellipse mit dem Format (x^2 / 9) + (y^2 / 16) = 1 berechnen

Question

Dieses mal soll ich durch inverse Integration eine Teilfläche einer Ellipse mit dem Format x² / 9 + y² / 16 = 1 im Bereich von -9/7 bis 3 berechnen (siehe Bild). Ich weiß aber nicht so richtig, wie man hier mit dem y und x umgehen muss, damit ich integrieren kann. Könntet ihr mir bitte helfen?

Answer 1

Bitte UNBEDINGT nachrechnen:

(14.4056)

Comments

Vorab schon mal vielen Dank. Das Ergebnis konnte ich bereits kontrollieren, und es stimmt tatsächlich.

Beim Lösungsweg kann ich jedoch einen Schritt nicht ganz nachvollziehen. Wie kommt man denn von 6 ∫ cos(2v)+1 du auf 6 • 0.5 (v+ cos(v) • sin(v)) + C ?

Kommt da irgendein spezielles Theorem zum Einsatz?

---

∫ cos(2v) dv

Substituiere

v=2x

dann bekommst Du  sin(v)/2

->Resubstitution

-->sin(2v)/2

sin(2v) =2 sin(v) cos(v)

damit bekommst Du

 sin(v) cos(v)

---

Ich vermute das dieses 1/2 durch den Halbkreis der Ellipse kommt, richtig?

Hier meine Rechnung.

---

@Martin

Welches 1/2 meinst du? Du hast doch selbst ein 1/2 vor dem Integral ab dem Moment, wo du aus dem dv ein du gemacht hast. Also aus der Substitution.

Was mir an deiner Rechnung gar nicht gefällt sind die Zeilen in denen du A= ... schreibst ohne ein Integral / ein +C oder | mit den Grenzen daneben. Die sind dann formal falsch.

Answer 2

Ich würde nach y auflösen nur den positiven Ast nehmen und den Funktionsterm von x (√(16 - 16x²/9) in den angegebenen Grenzen integrieren (Integralformelsammlung).