Ich hab eine kurze Frage zu dieser Aufgabe:
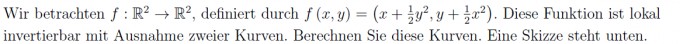
Für die Invertierbarkeit ist ja wichtig, dass die Determinante der Jacobi-Matrix ungleich 0 ist. Hier wollen wir ja wissen für welche x,y sie "0 wird".
Wir haben hier ja: det(Jf(x,y))=1-xy
Wir untersuchen daher: 0=1-xy
Dadurch erhalten wir x=1/y und y=1/x. Somit ist f an den beiden Kurven mit x=1/y und y=1/x. nicht lokal invertierbar.
Stimmt das ganze so?
lg