Die Frage nach dem Zeitpunkt identifiziert die Frage als Frage zu Vektoren. Das Schiff überwindet in einer Stunde eine Differenz \(d\) von
$$ d= S_1 - S_0 = \begin{pmatrix} 2\\0 \end{pmatrix}- \begin{pmatrix}5 \\ -3\end{pmatrix}= \begin{pmatrix} -3\\ 3 \end{pmatrix}$$
Daraus folgt die Schiffsroute \(s(t)\) des Frachters
$$s(t) = S_0 + t \cdot d = \begin{pmatrix}5 \\ -3\end{pmatrix} + t \begin{pmatrix}-3 \\ 3\end{pmatrix}$$
Wobei \(t\) die Zeit in Stunden nach passieren des Punktes \(S_0\) angibt. Und ein Bild sagt mehr als tausend Worte:
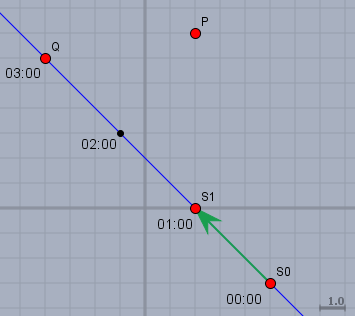
Ob die Route \(s(t)\) einen Punkt \(P\) bzw. \(Q\) trifft oder nicht, bekommt man heraus, wenn man überprüft ob die Gleichung \(s(t)=P\) eine Lösung hat.
$$s(t)=\begin{pmatrix}5 \\ -3\end{pmatrix} + t \begin{pmatrix}-3 \\ 3\end{pmatrix}=P=\begin{pmatrix}2 \\ 7\end{pmatrix}$$
hat keine Lösung, da \(t\) in der oberen Gleichung den Wert 1 hat
$$5 - 3t = 2 \quad \Rightarrow t =1$$
Und in der unteren den Wert \(10/3\) haben müßte. $$-3 + 3t = 7 \quad \Rightarrow t=\frac{10}{3}$$\(t\) kann aber nicht zwei Werte gleichzeitig annehmen. Für \(Q\) gilt
$$s(t)=\begin{pmatrix}5 \\ -3\end{pmatrix} + t \begin{pmatrix}-3 \\ 3\end{pmatrix}=Q=\begin{pmatrix}-4 \\ 6\end{pmatrix}$$
Diese Gleichung ist für \(t=3\) erfüllt. Folglich kommt das Schiff nach 3h (um 03:00Uhr) am Punkt \(Q\) an.