4b) Hochpunkt (-1|3) und Tiefpunkt T(1|-1) gegeben. Gleichung der Funktion bestimmen.

Question

Kann mir jemand die b erklären habe 2 Gleichung von 1 x Hoch- und 1 x Tiefpunkt da die Gleichung

f(x) = ax^3+bx^2+cx+d

Aber wie komme ich da weiter habe ja nur 2 Gleichungen

Comments

wo ist der rest?

---

vergessen ^^ ist drauf

---

Welche Aufgabe ganz genau ist gemeint?

Bitte Text jeweils auch sauber und vollständig als Text eingeben. https://www.mathelounge.de/schreibregeln Das erhöht die Wahrscheinlichkeit, dass jemand eine Antwort schreibt.

---

die b und nicht die c ,mein fehler

---

EDIT: Habe das nun in der Überschrift und in der Frage korrigiert.

---

Danke wollte es auch im nachhinein bearbeiten ging aber nicht mehr

---

Darf ich fragen, aus welchem Buch diese Aufgabe ist bzw. wie der Verlag heißt, bei dem das Buch erschienen ist? Dankeschön!

---

lambacher schweizer mathematik qualitfikationsphase grunkurs nrw

Answer 1

Nein, du hast 4.

Bilde erstmal die Ableitungen und setze die gleich 0 (das sind jeweils 1 Gleichung also 2 insgesamt).

Dann setzt du die Punkte (Hoch- und Tief-) in die allgemeine Gleichung ein und berechnest so die Koeffizienten. Das ist jeweils 1 Gleichung und somit 2.

Das ist ein nicht so schweres Problem.

Comments

welche ableitung soll ich 0 setzen ? 1 und 2 ?

wenn ich diese dann habe was soll ich dann mit der ableitung machen ?

---

beide

dann hast du zwei gleichungen. mit den anderen bedingungen insgesamt 4. das gl.sys. was du dann hast löst du (gesucht sind die koeffizienten)

---

ok habe die ableitung

f`x= 3ax^2+2bx+c

f´´x=6ax+2b

und die 2 gleichungen von den 2 punkten

a+b+c+d=-1

a-b-c+d=3

wie soll ich das rechnung kannst du mir das zeigen weiß nicht wie ich das mit den bedingungen machen soll bei den ableitungen ...

---

sry das ist nicht die c voll verpeilt das ist die nr b von der ich spreche

Answer 2

Falls du die Aufgabe b.) meinst

T ( 1 | -1 )
H ( -1 | 3 )

f ( x ) = a*x^3 + b * x^2 + c * x + d
f ´( x ) = 3a * x^2 2b * x + c

f ( 1 ) = -1
f ( -1 ) = 3
f ´ ( 1 ) = 0
f ´( -1 ) = 0

Bin gern weiter behilflich.

Comments

danke ! wie bist du da drauf gekommen

f ( 1 ) = -1 
f ( -1 ) = 3 
f ´ ( 1 ) = 0 
f ´( -1 ) = 0

das sind ja die 2 bedingungen  

braucht man nur die 1ste ableitung ? 
Ich habe jetzt noch die beiden gleichungen raus

a+b+c+d=-1

a-b-c+d=3

das sind ja die 2 bedingungen

---

f ( x ) = a*x³ + b * x² + c * x + d
f ( 1 ) = a*1³ + b * 1² + c * 1 + d  = -1
f ( -1 ) = a*(-1)³ + b * (-1)² + c * (-1) + d = 3

Im Hoch- bzw. Tiefpunkt ist die
Steigung = 1.Ableitung null.
f ´( x ) = 3a * x² 2b * x + c
f ´( 1 ) = 3a * 1²  + 2b * 1 + c = 0
f ´( -1 ) = 3a * (-1)² +2b * (-1) + c = 0

---

Zur Kontrolle

a + b + c + d = -1
-a + b - c + d = 3
3a + 2b + c = 0
3a - 2b + c = 0

f(x) = x^3 - 3·x + 1

---

Ich habe es so berechnet wie komme ich weiter

---

f ( 1 ) = a*1³ + b * 1² + c * 1 + d  = -1
ergibt sich durch ausmultiplizieren
f ( 1 ) = a + b  + c + d  = -1

f ( -1 ) = a*(-1)³ + b * (-1)² + c * (-1) + d = 3
ergibt sich durch ausmultiplizieren
f ( -1 ) = -a  + b - c + d = 3

f ´( 1 ) = 3a * 1² + 2b * 1 + c = 0
f ´( 1 ) = 3a  + 2b  + c = 0

f ´( -1 ) = 3a * (-1)² + 2b * (-1) + c = 0
f ´( -1 ) = 3a  - 2b  + c = 0

Answer 3

4b) Hochpunkt (-1|3) und Tiefpunkt T(1|-1) gegeben. Gleichung der Funktion bestimmen.

f(-1) = 3

f(1) = -1

f ' (-1) = 0

f ' (1) = 0

Das sind 4 Gleichungen. Nun noch einsetzen.

f(x) = ax³+bx²+cx+d

(I) -a + b - c + d = 3 

(II)  a + b + c + d = -1 

-------------------------------- (I) + (II) 

2b + 2d = 2  

f ' (x) = 3ax^2 + 2bx + c 

(III)  3a - 2b + c = 0

(IV) 3a + 2b + c = 0

------------------------------  (IV) - (III) 

4b = 0 

==> b = 0

Weil oben 2b + 2d = 2 ==> 0 + 2d = 2 ==> d = 1. 

usw. 

Comments

Wie hast du das eingesetzt und wie bist du auf die Bedigungen und dann auf die ABleitungen davon ?

---

In Hoch- und Tiefpunkten von Polynomen ist die erste Ableitung 0. Das kann und soll man verwenden.

Zum Ableiten habe ich Ableitungsregeln verwendet, die du eigentlich kennen solltest, wenn du solche Aufgaben üben sollst.

---

ah du hast recht das fällt dann ja weg aber wie bist du auf die funktion gekommen ?

---

Du findest inzwischen oben meine 4 Gleichungen und aus denen habe ich bereits 2 Parameter ausgerechnet. Nachrechnen und die andern beiden Parameter überlssse ich dir.

---

Okay die einzige frage die sich stellt ist wie bist du auf die hier gekommen

(III)  3a - 2b + c = 0

(IV) 3a + 2b + c = 0

wie hast du das berechnet ?

---

Ich hatte 4 Gleichungen: Nr. 3 und 4:

f ' (-1) = 0

f ' (1) = 0

---

ja du hast von den Bedingungen die Ableitung berechnet und hast das rausbekommen ,aber bei den gleichungen verstehe ich nicht ?

(III)  3a - 2b + c = 0

(IV) 3a + 2b + c = 012

---

Es gibt inzwischen 3 Antworten auf deine Frage.

Betrachte die morgen in Ruhe noch einmal und bastle daraus deine eigene Antwort.

Answer 4

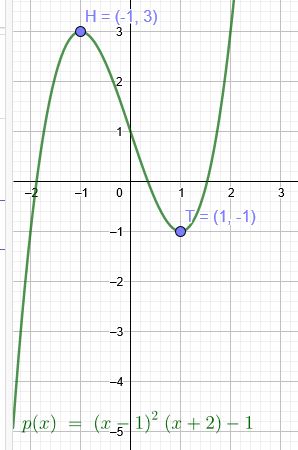
T \(( 1 | -1 )\)  und  H \(( -1 | 3 )\)

T \(( 1 | -1 )\) → T´ \(( \red{1} | 0 )\) doppelte Nullstelle und H \(( -1 | 3 )\)→ H´ \(( -1 | 4 )\)

\(f(x)=a(x-\red{1})^2(x-N)\)

H´ \(( -1 | 4 )\):

\(f(-1)=a(-1-1)^2(-1-N)=4a(-1-N)=4\)

\(a(-1-N)=1\)

\(a=\frac{1}{-1-N}\):

\(f(x)=\frac{1}{-1-N}[(x-1)^2(x-N)]\)

\(f'(x)=\frac{1}{-1-N}[(2x-2)(x-N)+(x-1)^2\cdot 1]\)

In jedem Hochpunkt ist eine waagerechte Tangente:

H´ \(( -1 | ... )\):

\(f'(-1)=\frac{1}{-1-N}[(-2-2)(-1-N)+(-1-1)^2]=0\)

\((-1-N)=1\)

\(N=-2\):

\(f(x)=(x-1)^2(x+2)\)↓

\(p(x)=(x-1)^2(x+2)-1\)

Comments

T \(( 1 | -1 )\) → T´ \(( \red{1} | 0 )\) doppelte Nullstelle und H \(( -1 | 3 )\)→ H´ \(( -1 | 4 )\)

Doppelte Nullstelle?

---

Doppelte Nullstelle?

Ja, weil dort jetzt der Tiefpunkt ist.

---

Aha, damit ist es klar. Du hast also die Funktion um eine Einheit nach oben verschoben. Ich hätte sie stattdessen um eine Einheit nach unten verschoben...