Welche Werte haben die Geschwindigkeitskonstanten für die Hin- und Rückreaktion?

Question

Aufgabe:

Für eine reversibele Reaktion \( A<->B \) mit \( [A]_{0}=100 \mu M \) und \( [B]_{0}=0 \) finden wir den unten dargestellten Verlauf.

Welche Werte haben die Geschwindigkeitskonstanten für die Hin- und Rückreaktion \( \left(k_{f}\right. \) und \( \left.k_{b}\right), \) wenn die gemessene Reaktionsgeschwindigkeitskonstante \( \left(k_{\text {obs }}\right) 0.09 \mathrm{~s}^{-1} \) und die finale Konzentration von \( \mathrm{A}\left([\mathrm{A}]_{\infty}\right) 11.11 \mu \mathrm{M} \) beträgt?

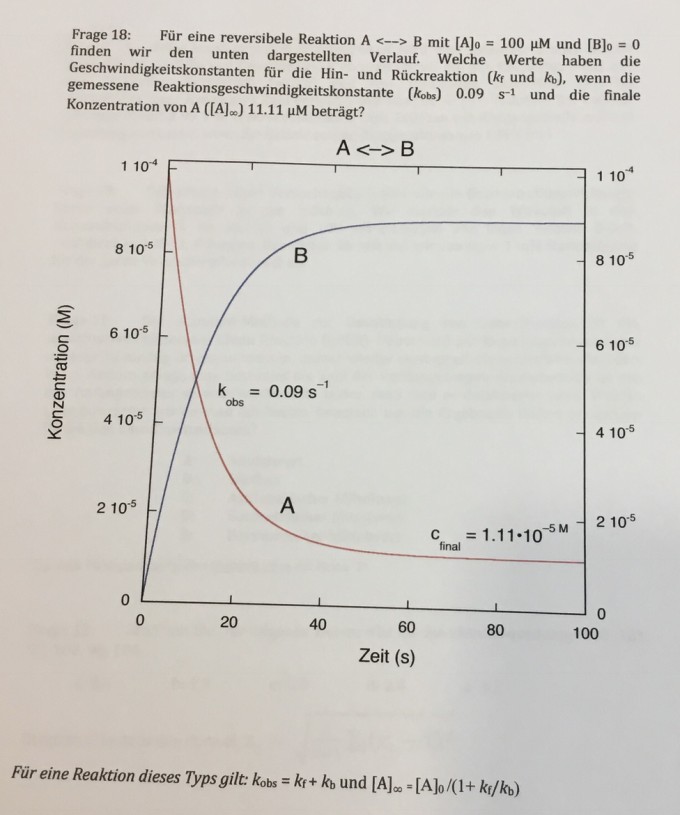
Was muss ich hier in welche Formel einsetzen? Habe versucht die gegebenen Werte einzusetzen, aber da kommt etwas falsches heraus.

Die Lösung ist Kf= 0,08 s^-1 und Kb=0,01 s^-1

Answer 1

Huhu! :-)

$$ A_{\infty} = \frac{A_0}{1+ \frac{k_f}{k_b}} \\A_{\infty}\cdot \left(1+ \frac{k_f}{k_b} \right) = A_0 \\A_{\infty} + A_{\infty} ~ \frac{k_f}{k_b} = A_0 \\\frac{k_f}{k_b} = \frac{(A_0 - A_{\infty})}{A_{\infty}} \quad \quad \bigg \vert    A_0 = 100, ~ A_{\infty} = 11.11, ~ k_f = k_{abs} - k_b \\\frac{k_{abs} - k_b}{k_b} = 8  \\k_b = \frac{k_{abs}}{9} = \frac{0,09}{9}\\\underline{\underline{{k_b = 0,01}}} $$

$$ k_f = k_{abs} - k_b = 0,09-0,01 \\\underline{\underline{{k_f = 0,08}}} $$

Comments

Ach ich hab falsch umgeformt deshalb hab ich nicht das richtige raus bekommen, dankeschön!!! :)