Hallo Tino,
ich habe den Zusammenhang mal in ein Koordinatensystem eingezeichnet. Deine Gleichung lautet (etwas umgestellt):
$$f(2-x)- \frac{2}{3} = -f(2+x) + \frac23$$
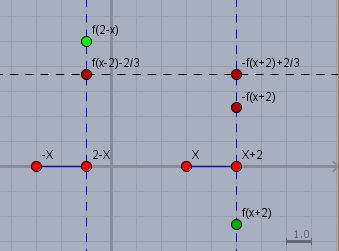
In der Skizze siehst Du zwei grüne Punkte, die jeweils das Koordinatenpaar \((2-x\space| \space f(2-x))\) und \((2+x\space| \space f(2+x))\) darstellen. Die Funktionswerte liegen genau so weit auseinander, dass die obige Gleichung erfüllt ist. Die Koordinate des X-Wertes habe ich frei gewählt.
Interessant ist der X-Wert bei dem \(2-x=2+x\) ist. Denn in diesem Fall ist \(f(2-x)=f(2+x)\). Aus
$$2-x=2+x \quad \Rightarrow 2-2=2x \quad \Rightarrow x=0$$
Für \(x=0\) gilt dann
$$f(2)- \frac{2}{3} = -f(2) + \frac23 \quad \Rightarrow f(2)=\frac23$$
Damit liegt schon mal ein Punkt der gesuchten Funktion fest.
Man kann aber auch anders an die Sache ran gehen. Dazu überlegt man sich vier Dinge:
1. was passiert, wenn man aus \(f(x)\) in \(f(-x)\) überführt? Spiegelung an der Y-Achse.
2. was passiert, wenn man aus \(f(x)\) ein \(-f(x)\) macht? Spiegelung an der X-Achse.
3. was passiert, wenn man aus \(f(x)\) ein \(f(x+a)\) macht? Verschiebung um \(a\) in negative X-Richtung.
4 was passiert bei \(f(x)\) wird zu \(f(x)+b\)? Verschiebung um \(b\) in positive Y-Richtung
dazu schau Dir folgende Skizze an
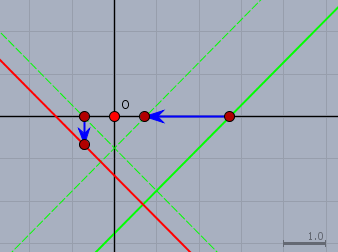
Angenommen, die grüne Gerade ist \(f(x)\). Dann verschiebe ich sie um -2 in X-Richtung \(\rightarrow f(x+2)\), spiegele sie an der Y-Achse \(\rightarrow f(-x+2)\) und um \(\frac23\) nach unten \(\rightarrow f(2-x)-\frac23\). Das Ergebnis ist die rote Gerade. (Edit: Bild und Absatz korrigiert)
Anschließend behandele ich die rechte Seite der Gleichung in der gleichen Weise geometrisch.

Verschieben um -2, Spiegeln an X und Anheben um 2/3 \(\rightarrow -f(x+2)+\frac23\). Das macht aus der grünen Geraden \(f(x)\) die rote. Nun muss aber natürlich \(f(x)=f(x)\) sein (das sind die grünen) und die roten müssen lt. der obigen Vorgabe gleich sein.
... hast Du 'ne Idee wie man weiter machen kann? Sonst frage nach!
Gruß Werner