Stammfunktion von (2+|x|)/x^2

Question

Wie lautet die Stammfunktion zu der Funktion (2+|x|)/x^2

Ich habe das vereinfacht: 2/x^2 + |x|/x^2 = 2/x^2 + 1/x

Stammfunktion ist dann -2/x + ln(x)

Ist das richtig?

Answer 1

So musst Du das wenigstens nicht erst in den Integralrechner einhämmern:

https://www.wolframalpha.com/input/?i=integral+(2%2B%7Cx%7C)%2Fx%5E2

Als Kontrolle: Bilde mal die Ableitung Deiner Stammfunktion.

Answer 2

Wie lautet die Stammfunktion zu der Funktion (2+|x|)/x² ?

Ich habe das vereinfacht: 2/x² + |x|/x² = 2/x² + 1/x

Tja, was soll man dazu sagen?
Die "Vereinfachung" ist falsch!
Es ist

$$y' = \dfrac{2}{x^2} + \dfrac{1}{\left|x\right|}.$$

Answer 3

https://www.integralrechner.de/

Comments

Bravo!                          

Answer 4

Machen wir doch die gute alte Fallunterscheidung

(2+|x|)/x²

Für x ≥ 0 gilt
f ( x ) = ( 2 + x ) / x^2
f ( x ) = 2 / x^2 + 1  / x

Stammfunktion ln(x) - 2/ x

Für x < 0 gilt
f ( x ) = ( 2 + x * (-1) ) / x^2
f ( x ) = ( 2 - x ) / x^2
f ( x ) = 2 / x^2 + 1  / x

Stammfunktion - ln(x) - 2/ x

Es gibt also 2 Stammfunktion

Für x ≥ 0 gilt
Stammfunktion ln(x) - 2/ x

Für x < 0 gilt
Stammfunktion - ln(x) - 2/ x
Da x immer > 0 im Logarithmus sein muß
ist die Definitionsmenge D =  { }
Es gibt keine Stammfunktion für x < 0.

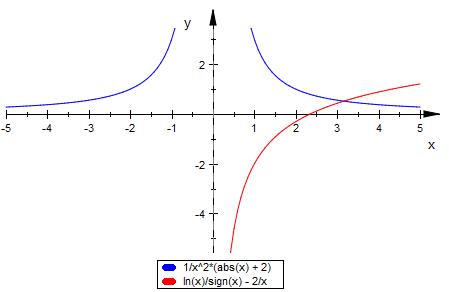
Graph Matheprogramm
blau : die Funktion
rot : die Stammfunktion

Comments

Es gibt also 2 Stammfunktion 

Nicht nur 2 !

Es gibt keine Stammfunktion für x < 0. 

Da würde ich an deiner Stelle nochmal nachdenken.

---

Für x ≥ 0 gilt
Stammfunktion ln(x) - 2/ x
Eher nicht.