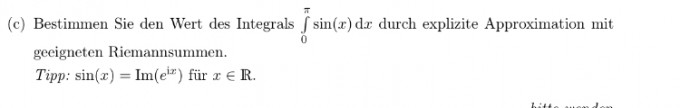Vom Duplikat:
Titel: Wert des Integrals berechnen
Stichworte: berechnen,integralrechnung,integral
Hallo kann mir jemand zeigen wie man das mit explezite Approximation mit geeigneten Riemannsummen man weil ich kann das nur mit den Haupsatz:
=-cos(x) [0,pi] = -cos(pi) -(cos(0)=2