Extremwertaufgabe pythagoräischen lehrsatz

Question

Einer Kugel mit dem Radius R=6 cm ist ein gerader Kreiszylinder von größtem Volumen einzuschreiben. (Lös:r=4.9cm, h=6.93cm)

Comments

V(r, h)  =  π* r^2* h.

---

Schon klar, aber ich weiß nicht wie ich weitermachen soll und wie man auf das Ergebnis kommt

---

Dazu legen wir eine Schnittebene durch Kugel und Zylinder, die normal auf die Deck- und Bodenfläche des Zylinder steht und durch den Kugelmittelpunkt geht. In ihr kann der Zusammengang zwischen r und h einfacher abgelesen werden als in einer Skizze der räumlichen Situation . Ein rechtwinkeliges Dreieck ist hervorgehoben: Über den Pythagoräischen Lehrsatz offenbart es die gesuchte Beziehung:

r^2+(h/2)^2=R^2 (Radius des Kreises (R))

---

Danke aber ich weiß nicht wie man auf 4.9 und 6.93 kommt :/. Wie soll das gehen, wenn ich nur R=6cm habe? 

Answer 1

Hier eine Skizze

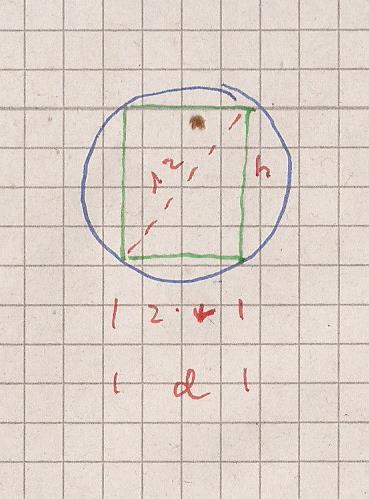
Kugel : 6 cm Radius entspricht Durchmeser = 12 cm
h ist die Höhe
Unten :  d ist der Durchmesser des Zylinders.

12 ^2 = h^2 + d^2
d^2 = 12 ^2 - h^2

V ( Zylinder ) = d^2 / 4 * π * h
V ( Zylinder ) = ( 12^2 - h^2 ) / 4 * π * h
V ( Zylinder ) = ( 12^2 * h -  h^3 ) / 4 * π
V ´( h ) = 1/ ( 4 * π ) * [ 12^2 - 3 * h^2 ]
Extremwert
12^2 - 3 * h^2 = 0
h = 6.93 cm

d^2 = 12 ^2 - 6.93 ^2
d = 9,8 cm
r = 4.9 cm

Comments

Ahh omg ich habs verstanden. Dankeeee 

---

Dazu ist das Forum da.
mfg Georg