Ich habe folgende Gleichung:
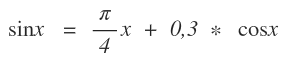
Ich muss die Gleichung mit dem Startwert x = -1,0 lösen. In der Aufgabe ist angegeben, dass man die direkte Fixpunktgleichung nutzen soll und zwar ohne Verwendung einer asin oder acos Funktion, den Gegenfunktionen von sin und cos.
Bei einem besprochenen Beispiel haben wir das nur einmal mit der Gegenfunktion gemacht. Jetzt frage ich mich, wie ich das hier anstellen soll.
Ich freue mich auf eure Tipps!
Gruß - Bear
