Näherungsparabel Exponentialfunktion

Question

Betrachtet wird die Funktion f(x)=(x-1) •e^x

Bestimmen Sie die Gleichung der näherungsparabel g(x)=ax^2+bx+c, die mit dem Graphen von f im Wendepunkt, im Tiefpunkt und in der nullstelle von f übereinstimmt .  

Ich verstehe diese Aufgabe nicht kann mir jemand bitte helfen ? 

 

Answer 1

Hallo Rehan,

Die Ableitungen der Funktion \(f(x)=(x-1)e^{x}\) sind

$$f'(x)=x \cdot e^{x}$$ $$f''(x)=(x+1) \cdot e^{x}$$ folglich liegt der Tiefpunkt bei \((0|-1)\) und der Wendepunkt bei \((-1|-2e^{-1})\). Die Nullstelle von \(f(x)\) liegt bei \(x=1\). Es ist eine Parabel gesucht, die durch diese drei Punkte geht. Setzte dazu jeden der drei Punkte in die allgemeine Gleichung einer Parabel ein.

$$a \cdot 0^2 + b \cdot 0 + c = -1$$ $$a \cdot (-1)^2 + b \cdot (-1) + c = -2e^{-1}$$ $$a \cdot 1^2 + b \cdot 1 + c = 0$$ Dies ist ein lineares Gleichungssystem mit der Lösung \(a=1-e^{-1}\), \(b=e^{-1}\) und \(c=-1\). Graphisch sieht das so aus

~plot~ (x-1)*exp(x);(1-exp(-1))x^2+(exp(-1))x-1 ~plot~

Gruß Werner

Comments

In der Kürze liegt die Würze :-)

---

"In der Kürze liegt die Würze" Stimmt - guckst Du hier oder das mit den Bakterien. Es ist nicht so einfach die Vorlieben der Fragenden zu treffen ;-)

Die Frage ist doch, ob das überhaupt sinnvoll ist!? Aber Hauptsache es macht Spaß.

Answer 2

Hallo Rehan,

f(x) = (x-1) * e^x  = 0   →   x = 1   →   Nullstelle (1 | 0)

f '(x) = x * e^x = 0  →  x = 0  mit VZW   →  T(0 | -1)

f "(x) = (x + 1) * e^x = 0  mit VZW  →  W( -1| - 2/e )  ≈  (-1| -0.736 ) 

g(x) = ax² + bx + c  mit

g(1) = 0     ⇔  a + b + c = 0

g(0) = -1    ⇔  c = -1

g(-1) = -2/e    ⇔  a - b + c = -2/e  

bleiben 

a + b  =  1                        [  →  b = 1 - a ]

a - b  = 1 - 2/e     , addieren:

2a = 2 - 2/e   | : 2

a = 1 - 1/e     →   b = 1/e 

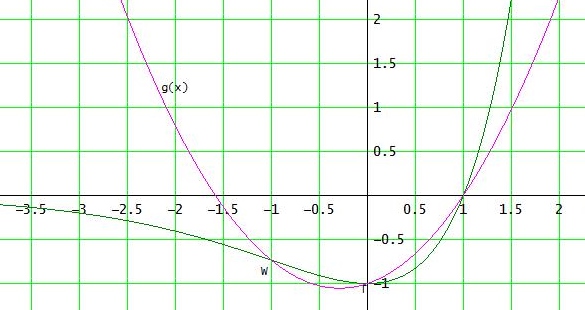
g(x)  =  (1-1/e) * x² + 1/e * x - 1     (  ≈  0.632·x² + 0.36·x - 1 )

Gruß Wolfgang