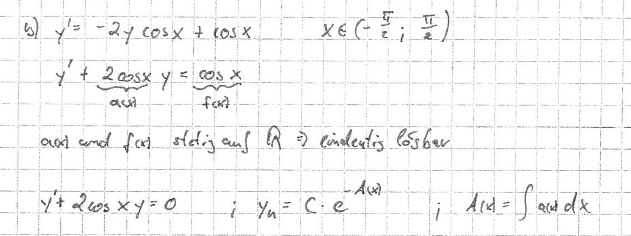Differentialgleichung lösen. y´= -2y cosx + cosx

Question

Es soll die allgemeine Lösung bestimmt werden.

Ich habe es gerechnet aber meine Lösung sieht anders als die richtige aus.

Was habe ich falsch gemacht.

Kann man es überhaput so rechnnen wie ich es gemacht habe?

Oder muss man diesen WEg mit a(x) und f(x) gehen, so wie es in der Lösung dargestellt ist.

Allerdings verstehe ich nicht was da gemacht wird.

Meine Lösung:

Richtige Lösung

Answer 1

Hallo Frost,

Kontrolllösung:

https://www.wolframalpha.com/input/?i=y+%27+%3D+-+2y+*+cos(x)+%2B+cos(x)

Du kannst auch einfach die Variablen trennen:

y ' = -2y * cos(x) + cos(x)  = cos(x) * (-2y + 1)  | : Klammer

y ' /  (-2y + 1) =  cos(x) 

dy/dx * 1 / (-2y + 1)  = cos x 

∫ 1 / (-2y + 1)  dy  =  ∫  cos(x)  dx

Gruß Wolfgang

Answer 2

Der allgemeine Weg  mit dem cos(x) ausklammern ist  richtig.

Kann es sein, das das ∫ cos(x) = - sin(x) +C bei Dir falsch ist?

Das Integral ist doch sin(x) +C

Comments

ok stimmt.

dann komme ich darauf.

Bei letzten Schritt, wo ich mit "2" teilen muss, kann ich aus C/2 = C machen richtig?

Keine Ahnung warum das Bild hier gedreht wird,

---

Bei letzten Schritt, wo ich mit "2" teilen muss, kann ich aus C/2 = C machen richtig?

->JA , das stimmt, besser C₁

_{Du kannst auch 1/2 ausklammern}