Das Glücksrad wird sechsmal gedreht. Wie groß ist die Wahrscheinlichkeit, dass genau zweimal grün erscheint?

Question

Ich habe da eine Frage zu dieser Aufgabe (s. unten). Ich habe sie gelöst, aber da kommt eine falsche Lösung raus. Und ich weiß nicht, wo mein Fehler ist. Ich hoffe jemand kann mir helfen!

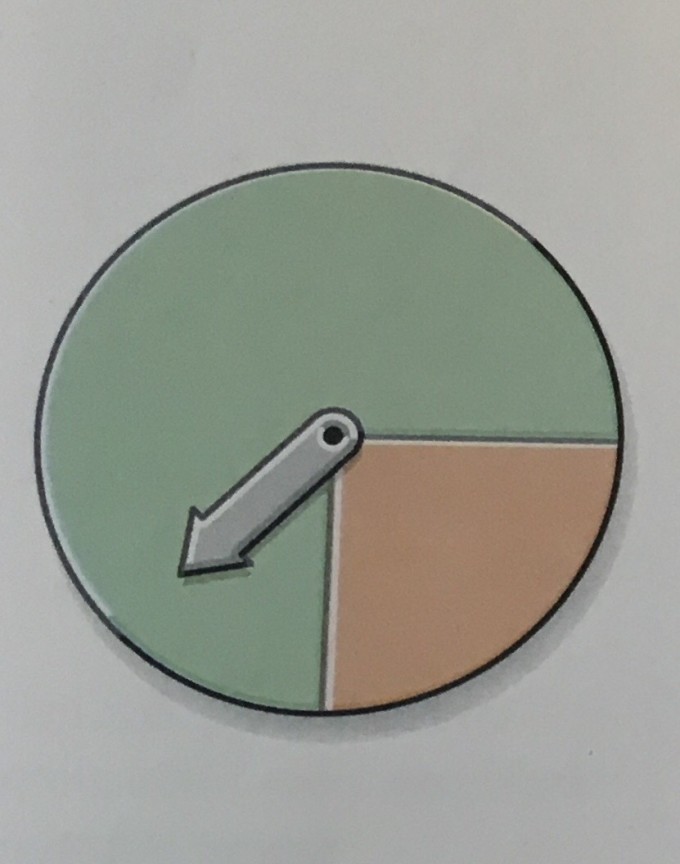
Auf dem Bild seht ihr das Glücksrad und die Aufgabe, wie ich sie gelöst habe.

Das Glücksrad wird sechsmal gedreht. Wie groß ist die Wahrscheinlichkeit, dass genau zweimal grün erscheint?

Answer 1

(6über2)*(3/4)^2*(1/4)^4  = ...

Comments

Genau so habe ich es gemacht, aber da kommt eine negative Lösung raus. Weißt du vielleicht warum?

---

Nein!

≈0.03295898438

Du rechnest mit Bruchstrich!!!

Es gibt auf deinem Taschenrechner eine Taste, die heißt "nCr". Die musst du so drücken:

(6 [nCr] 2)*(3/4)^2*(1/4)^4

sonst normal bruchstrich.

---

Du solltest dir nochmal genau ansehen wie man Binomialkoeffizienten ausrechnet:

(6über2)=6!/(2!*4!)=720/(2*24)=15

---

Ja genau, das soll rauskommen, also 0,032...

Dankeschön, das hat mir geholfen!

---

(6über2)=6!/(2!*4!)=720/(2*24)=15

Woher kommt denn jetzt die 4!?

Müsste da nicht nur 2 aufgrund der Anzahl der Treffer stehen?

---

(6über2)=6!/(2!*4!)=720/(2*24)=15

Woher kommt denn jetzt die 4!?

Müsste da nicht nur 2 aufgrund der Anzahl der Treffer stehen?

---

(n über k)= n! / (k! * (n-k)!)

Das ist die Formel für den Binomialkoeffizienten. Hier wird für n die 6 eingesetzt und für k die 2.