Additionstheorem cos(x+y) mit der Eulerschen Formel beweisen

Question

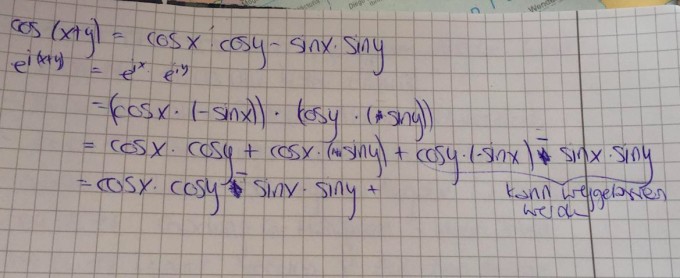
leider haben ich schon in diversen Foren nach der Lösung gestöbert und auch Wolfram Alpha verwendet, bloß finde ich nichts hierzu.

Kann mir einer bei meinem Problem weiterhelfen? Meinen Lösungsweg bestätigen oder ausbessern? Mich auf eventuell Fehler hinweisen?

PS: Der Term, der als "kann weggelassen werden" markiert ist war meine eigene Vermutung. Sprich ich habe angenommen das der Additionstheorem cos(x+y) nur bewiesen werden kann, wenn der imaginär Teil wegfällt. Jedoch bin ich mir unsicher, was das angeht.

Danke

Answer 1

Hallo

 benutze $$cos(x+y)=(e^{i*(x+y)}+e^{-i*(x+y)})/2$$

dann wie bei dir $$e^{i}x*e^{iy}=(cos(x)+isin(x))*(cos(y)+isin(y))$$ für die 2 Ausdrücke und addiere.

Auf deinem Zettel seh ich kein i,

du kannst natürlich auch einfach den Realteil von $$ e^{ix}*e^{iy} $$ benutzen. wenn du das richtig aufschreibst. Auf deinem Zettel ist nur durcheinander! was hat  etwa $$cos(x)\cdot(-sin(x)) \quad mit \quad e^{ix} zu tun$$ Gruß lul

Comments

dachte, das der term für e^ix geht.. Lag wohl sehr falsch.

Danke für die Verbesserungen :)