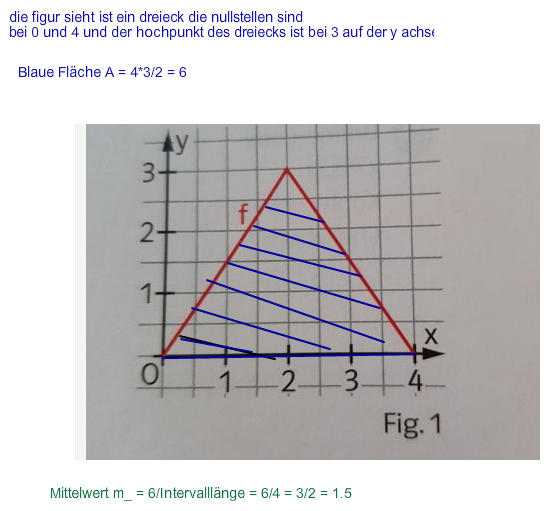
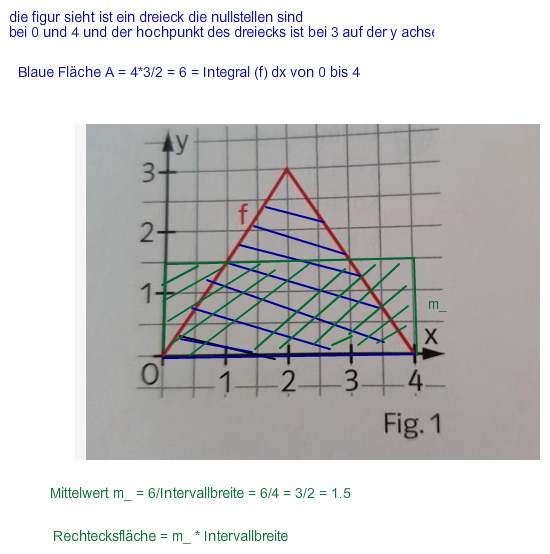
Die obere Zacke mit dem "Hochpunkt" wird zweigeteilt, gedreht und rechts und links zum grünen Trapez hinzugefügt. ==> Man bekommt ein Rechteck mit gleicher Fläche, wie das gegebene Dreieck.
Beachte zusätzlich
m_ hat ein Vorzeichen (oben PLUS), gleich wie das bestimmte Integral.
Das "Ersatzrechteck" (grün) ist also entweder oberhalb oder unterhalb der x-Achse.
D.h. im Bild müsste "orientierte Fläche" stehen, wo einfach Fläche steht.