Ermitteln Sie die Stellen der Tangente

Question

f(x)= (1/48)x³ -(3/8)x² + (27/16)x +1

a) Ermitteln sie rechnerisch eine Gleichung der Geraden S die durch die Punkte H(3|13/4) und T(9|1)

Meine LosufL zu a) y= -(3/8)*x+(35/8)

b) Es gibt zwei Stellen an denen der Graph von f Tangenten hat die parallel zu gerade S verlaufen ermitteln Sie diese Stellen auf 2 Nachkommastellen genau

Ich benötige Hilfe bei der b

Answer 1

Hallo

parallel heist ja gleiche Steigung: also suchst du die Stellen mit f'(x)=-3/8 , was eine quadratische Gleichung ergibt.

Gruß lul

Answer 2

f(x)= (1/48)x³ -(3/8)x² + (27/16)x +1

Falls es stimmt das die Steigung - 3/8 ist
dann gilt dies auch für die Tangenten

f ´( x ) = -3/8
f ´( x )= 3/48 *x^2 -6/8 *x + 27/16
f ´( x )= 3/48 *x^2 - 6/8 *x + 27/16 = -3/8
Mitternachforml / pq-Formel / quadrat.Ergänzung
x = 7.732
und
x = 4.268

f ( 7.732 ) = 1.259
B ( 7.732 | 1.259) mit Steigung -3/8

y = m * x + b
1.259 = -3/8 * 7.732 + b
b = 4.159

1.Tangente
t1 ( x ) = -3/8 * x + 4.159

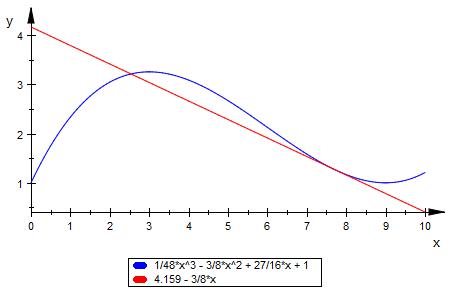
Bei Bedarf nachfragen.
2.Tangente
( 4.268 | 2.991 )
f ( x ) = -3/8 * x + 4.592