Bestimmen Sie die Funktion f und skizzieren Sie die 1. Ableitung in das KS (oHiMi = ohne TR)

Question

Hallöchen liebe Community,
kann mir bitte jemand erklären wie man an solchen Aufgaben herangeht und wie man bei solchen komplizierten Funktionen die Gleichungen anhand der Skizze ermittelt? Wenn möglich, dann bitte ausführlich, damit ich es mir für die Zukunft notieren kann.

Einige Dinge habe ich jedoch durch meine lange Schullaufbahn erkannt, sonst wäre es ja viel zu traurig haha.
Die Funktion hat 4. Nullstellen, also ist es die Funktion des 4. Grades. Ich erkenne eindeutig einzelne NS, so kann ich mit Linearfaktorzerlegung arbeiten.

$$ (x+3) • (x-1) • (x-3) • (x-6) $$
Jetzt stellt sich nun heraus, wie ich diese Funktion so stauchen (ich weiß nicht, ob es ein richtiger Begriff dafür ist) kann, dass es wie auf dem Bild aussieht. Allerdings weiß ich nicht welche Zahlen ich dafür nehmen muss und wo genau in der Gleichung der Linearfaktorzerlegung einsetzen muss. Es ist eine oHiMi Aufgabe, wir dürfen nicht mit dem CAS TR arbeiten.

Ich hoffe wirklich sehr, dass mir jemand das gut erklärt, ich würde mich darüber außerordentlich freuen, denn ich möchte in der Zukunft bessere Noten schreiben.

Euch noch einen schönen und produktiven Start in die Woche!

LG 

Comments

Ich zweifle an der Nullstelle x=6 und würde eher einen Hochpunkt (2|2) annehmen. Leider ist die Zeichnung allerdings eher schlecht zu deuten.

---

Ja tut mir leid, eine bessere Zeichnung habe ich nicht. Diese haben wir zur LK bekommen. Ich weiß auch nicht, was unsere Lehrerin sich dabei gedacht hat. 

---

Bei der Aufgabe kann man vermutlich nicht viel retten, das Bild ist dermaßen miserabel gedruckt, dass man zu wenige Punkte eindeutig ablesen kann.  Nur (2,2) ist eindeutig erkennbar. Deine Nullstellen könnten stimmen, aber das lässt sich höchstens mit dem Lineal nachprüfen.

---

Leider ist der Verlauf des Graphen recht empfindlich gegenüber kleineren Änderungen an den Bestimmungsdaten, der erste Teil der Aufgabe ist daher schon mal kaum sinnvoll bearbeitbar. Um die Ableitung zu skizzieren, reicht die Qualität der Zeichnung allerdings aus.

Answer 1

f ( x ) = a * ( x + 3 ) * ( x -1 ) * ( x - 3 ) * ( x - 6 )
Ein ganzzahliger Punkt ( 2 | 2 )
f ( 2 ) = a * ( 2 + 3 ) * ( 2 -1 ) * ( 2 - 3 ) * ( 2 - 6 ) = 2
a * ( 5 ) * ( 1 ) * ( - 1 ) * ( -4 ) = 2
a * ( 20 ) = 2
a =  0.1

f ( x ) =  0.1 * ( x + 3 ) * ( x -1 ) * ( x - 3 ) * ( x - 6 )

Comments

Ich habe gerade mit dem TR überprüft, leider stimmt das noch nicht so ganz. Der globale Tiefpunkt liegt nach Ihrer Rechnung unter der -12. Nach der Skizze aber, müsse er über die -12 liegen, also nicht genau auf -12. Aber wir kommen auf jeden Fall immer näher. :-)

---

Ich habe deine Werte übernommen.
Falls du ein genaueres Ergebnis haben
willst dann mußt du mit dem Lineal
die Nullpunkte ausmessen.
Ob mit Fließkommazahlen allerdings ein
Ergebnis noch ohne Taschenrechner zu
ermitteln ist ?

Auf jeden Fall weißt du jetzt wie man eine
Funktion, unter Beibehaltung der Nullstellen,
noch Stauchen oder Strecken kann.
1 Punkt der Kurve entnehmen und einen
Streckungsfaktor einführen.

---

Zur Weiterbildung zum Abiturniveau

Hinweis : bei

http://www.abiturloesung.de/

gibt es in schriftlicher Form : Abiturklausuren ( Grund- und Leistungskurs ) deren Lösungen
Schritt für Schritt sowie Unterrichtsstunden auf Video dazu. Ich konnte dort eine Menge lernen.

Answer 2

Du hast offenbar zwei Teilaufgaben.

Wenn da steht 1. Ableitung "skizzieren" ohne Hilfsmittel. Brauchst du keine Funktionsgleichung zu rekonstruieren.

Hier mal die Nullstellen der 1. Ableitung:

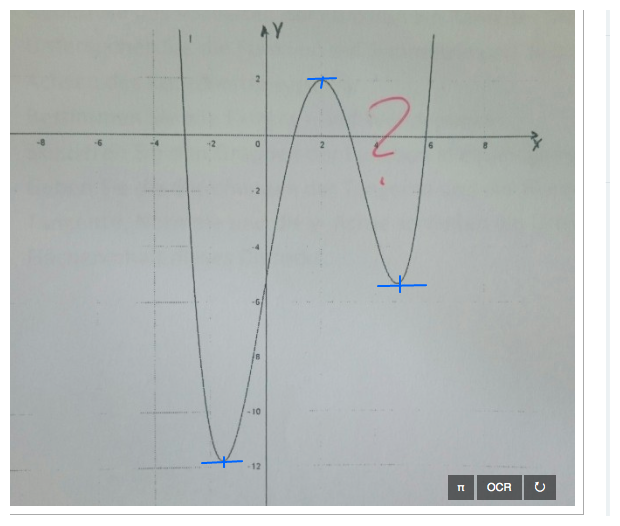
Somit weisst du, dass f' durch die 3 Kreuzchen geht.

Weitere Punkte auf dem Graphen der Ableitung bekommst du mit Steigungsdreiecken.

Ich habe mal 2 eingezeichnet. Aber du musst das auf dem Original genauer machen.

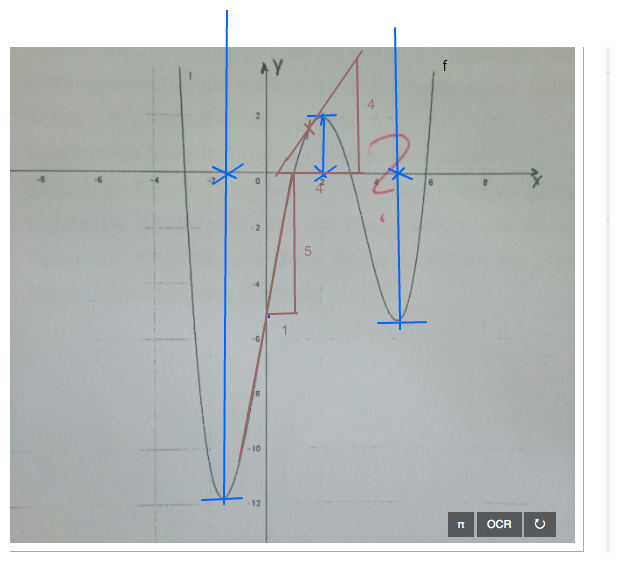
Zwei weitere Punkte (blaue Kreuzchen)

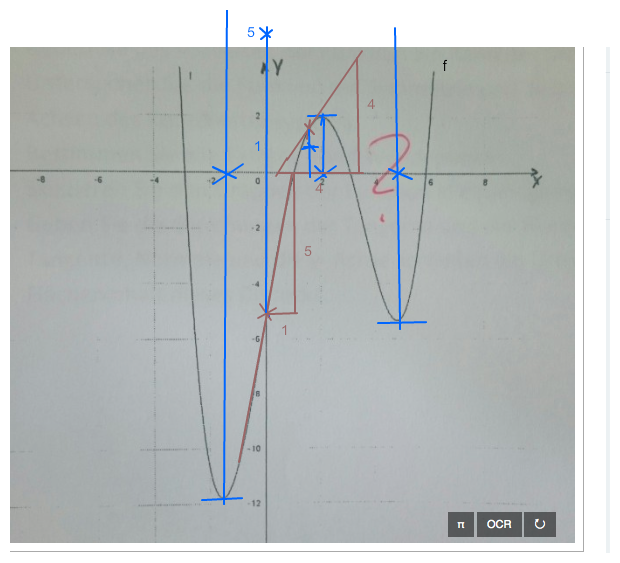
Nun noch mehr Punkte einzeichnen und dann schwungvoll gebogen verbinden (ohne Ecken).

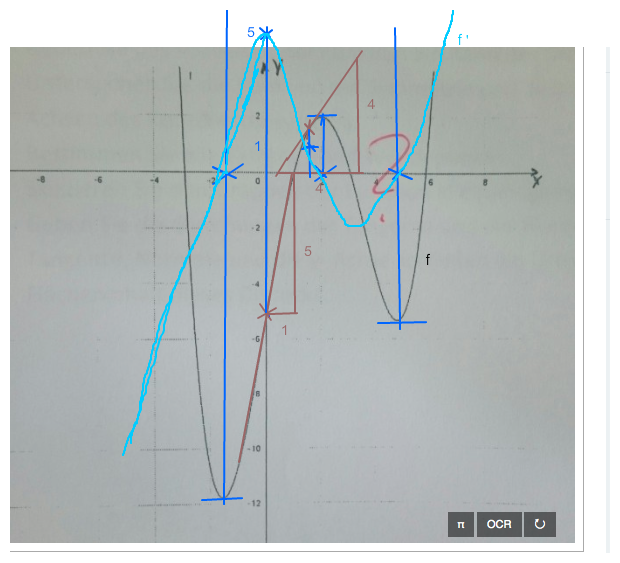
Zwischen x=-2 und x=0 natürlich nur ein Bogen (linke Linie passt ungefähr (rechte daneben bitte ignorieren))

Graph von f ' sieht aus wie ein Polynom 3. Grades. --> Passt ungefähr.

Comments

Dankeschön für Ihre Mühe! :-)

---

Bitte schön.