Ja - es gibt beliebig viele Punkte wie Du den Teppich so aufhängen kannst. In jedem Fall sollte sich die Oberkante des Teppichs an der Decke befinden und je eine der unteren Ecken an je einer der beiden Seitenwände der Ecke. Zur Beschreibung der Lage des Teppichs wähle ich zwei Winkel \(\alpha\) und \(\beta\). \(\alpha\) soll beschreiben in welchem Winkel der Teppich von der linken Wand weg hängt. Ist \(\alpha=0\) so hängt er ganz an der linken Wand, ist \(\alpha=45°\) so hängt er symmetrisch zur Ecke und ist \(\alpha=90°\), so hängt er an der rechten Wand. \(\beta\) soll beschreiben, wie weit der Teppich nach vorn geneigt ist. Ist \(\beta=0°\), so hängt er senkrecht und ist \(\beta=90°\) so würde er flach an der Decke hängen (aber das willst Du nicht). (Bem.: links und rechts beziehen sich auf den Betrachter!)
Weiter führe ich ein Koordinatensystem ein. Der Ursprung liegt in der Zimmerecke an der Decke. Die X-Achse verläuft an der linken Wand und die Y-Achse an der rechten Wand. Die Z-Achse geht nach oben - d.h. wir werden später nur negative Z-Koordinaten haben.
Die Abmessungen des Teppichs seien \(b=1,5\text{m}\) und \(h=1,5 \text{m}\). Dann liegen die untere linke und rechte Ecke bei
$$e_{lu} = \begin{pmatrix} b \cdot \cos \alpha \\ 0 \\ -h \cdot \cos \beta \end{pmatrix}$$
$$e_{ru}= \begin{pmatrix} 0 \\ b \cdot \sin \alpha \\ -h \cdot \cos \beta \end{pmatrix}$$
Die oberen Ecken sind etwas schwieriger:
$$e_{lo} = \begin{pmatrix} b \cdot \cos \alpha + h \cdot \sin \beta \cdot \sin \alpha\\ h \cdot \sin \beta \cdot \cos \alpha \\ 0 \end{pmatrix}$$
$$e_{ro} = \begin{pmatrix} h \cdot \sin \beta \cdot \sin \alpha\\ b \cdot \sin \alpha + h \cdot \sin \beta \cdot \cos \alpha \\ 0 \end{pmatrix}$$
Folgendes Bild zeigt ein Beispiel mit \(\alpha=30°\) und \(\beta=15°\)
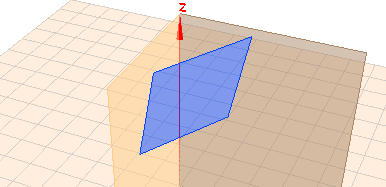
Klicke auf das Bild, dann kannst Du die Szene mit der Maus drehen. Das verschafft Dir einen räumlichen Eindruck.
Falls Du Fragen hast, so melde Dich bitte.
Gruß Werner