Ein Rhombus (oder Raute) ist ein Viereck, bei dem u.a. die Diagonalen auf einander senkrecht stehen. Die entstehende Figur sollte also etwa so aussehen:
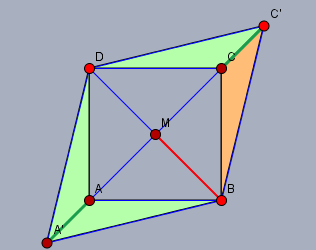
Die grün markierten Strecken \(|A'A|\) und \(|CC'|\) sollen 1,2m lang sein. Die farbig (grün und orange) markierte Fläche soll in Summe 8m2 groß sein. Folglich ist aus Gründen der Symmetrie die Fläche des orange markierten Dreiecks \(\triangle C'CB\) ein Viertel davon, also 2m2 groß. Die Strecke \(|MB|\) (rot) ist die halbe Diagonale und glechzeitig die Höhe von \(\triangle C'CB\) über \(C'C\). Es gilt also für die Fläche dieses Dreiecks:$$F_{\triangle C'CB} = \frac12 \cdot 1,2\text{m} \cdot |MB| = 2\text{m}^2 \\ \space \Rightarrow |MB| = \frac{10}{3} \text{m}$$
Daraus folgt die Länge der Diagonale des Quadrats \(|DB|\) und die Länge der größeren Diagonale \(|A'C'|\) des Rhombus: $$|DB| = 2|MB| = \frac{20}{3} \text{m} \approx 6,667 \text{m}\\ |A'C'| = |DB| + 2 \cdot 1,2\text{m} = \frac{136}{15}\text{m} \approx 9,067 \text{m}$$