Messe den horizontalen Abstand zwischen zwei Wellenbergen, die Wellenlänge \(l=3\) (bzw. Periodendauer), die halbe Höhe der Welle \(A=1\), sowie den "Start" \(t_0\) der Cosinus-Funktion; also den x-Wert, an dem die Funktion den Wert von \(\cos(0)=1\) annimmt.
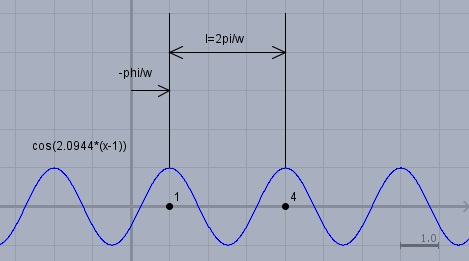
Dann ist $$A= 1 \\ \omega = \frac{2\pi}{l} = \frac23 \pi \\ \varphi = - \omega \cdot t_0 = - \frac23 \pi \cdot 1 = -\frac23 \pi$$ die Funktion lautet folglich $$f(t) = 1 \cdot \cos\left( \frac23 \pi(t - 1)\right)$$ Gruß Werner
