Zeigen Sie, dass (T, ⊕, ∗) sogar ein kommutativer Ring ist und dass die Teilmenge I ein Ideal von T ist!

Question

Sei T:= {\( \begin{pmatrix} a & 0 \\ 0 & a \end{pmatrix} \) | a ∈ ℤ}

Wir bezeichnen mit ⊕ und ∗ die Matrizenaddition und -multiplikation und definieren α : ℤ → T, für alle z ∈ Z sei z^α := \( \begin{pmatrix} z & 0 \\ 0 & z \end{pmatrix} \). Sie dürfen wissen, dass (T, ⊕, ∗) ein Ring ist.

Zeigen Sie, dass (T, ⊕, ∗) sogar ein kommutativer Ring ist und dass die Teilmenge

I := { \( \begin{pmatrix} 2b & 0 \\ 0 & 2b \end{pmatrix} \) | b ∈ ℤ} ein Ideal von T ist!

Mein Ansatz:

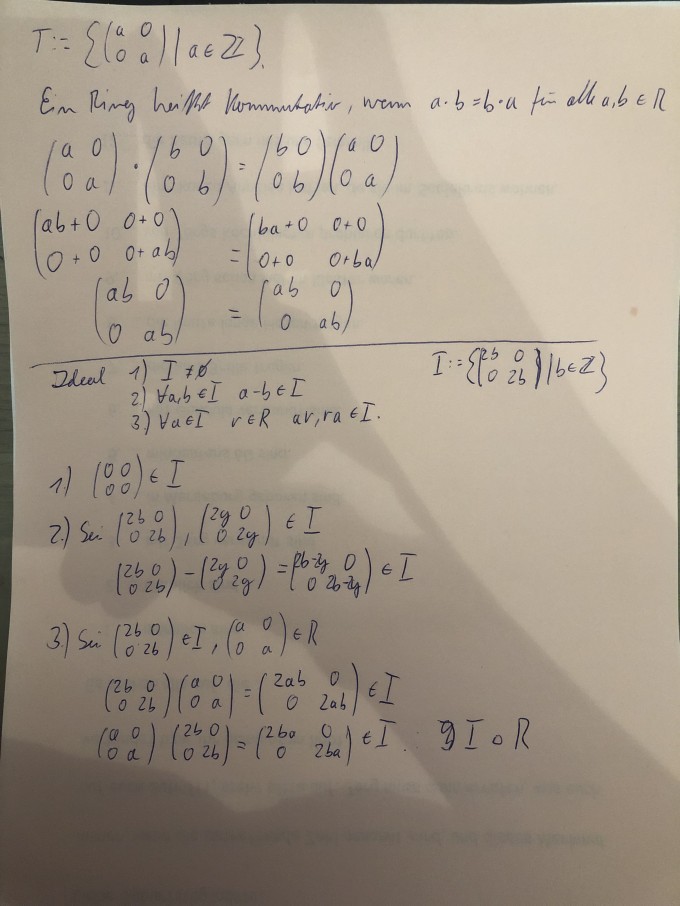
Kann man das so machen, oder ist das totaler Blödsinn? Freue mich über eure Hilfe!

Answer 1

Hallo Gast, Teil 1, kommutativer Ring, ist korrekt.  Teil 2, Ideal: 
Laut Wikipedia ist bei Idealen folgendes zu klären:
• Enthält I das Nullelement?  Ja
• Ist I abgeschlossen gegenüber der Addition?  Ja.  Du zeigst Subtraktion, aber egal.
• Ist I abgeschlossen gegenüber der Multiplikation?  Ja.  Das wäre noch zu zeigen.  Aber ist mit dem nächsten Punkt automatisch erledigt.
• Ist I abgeschlossen, wenn man es mit einem bel. Element von T multipliziert?  Ja.  Du schreibst R, aber meinst T.

Für was braucht man die von dir angegebene Abbildung α?  Keine Ahnung.