da ich mich in der 9ten Klasse schon intensiv für die Abschlussprüfung der 10ten vorbereite, löse ich Prüfungsaufgaben.
Bei dieser hier habe ich ein paar Probleme
Aufgabe:
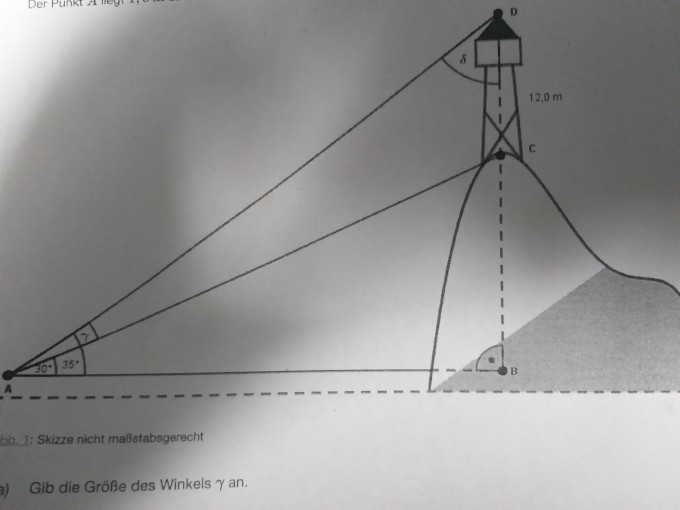
Tim möchte mit einem Messgerät die Höhe des Hasen Werks bestimmen. Auf der Bergspitze C befinden sich eine 12,0 Meter hohe Aussichtsplattform D. Vom Punkt A misst er die zwei Winkelgrößen 30 Grad und 35 Grad. Der Punkt A liegt 1,5 Meter über dem Boden
Gib die Größe des Winkels Gamma an
Tim gibt die Größe des Winkels delta mit 55° an begründet die Richtigkeit von Tims Angabe
Tim hat für Strecke AC eine Länge von 112,8 m bestimmt
Bestätige diese Angabe durch eine geeignete Rechnung
ermittle die Höhe des Hasenberges
Gib an auf welcher Höhe über dem Boden sich die Aussichtsplattform D befindet
Problem/Ansatz:
Leider haben wir das Thema noch nicht wirklich behandelt, deshalb bin ich daran interessiert vor zu arbeiten, damit ich von Anfang an durchblick habe!
Eine kurze Erklärung zu der jeweiligen Rechnung würde mir reichen