Hallo ich kann nicht durch diese Aufgabe.
Die Aufgabe lautet:
Untersuchen Sie die Funktion f(x) = |xsin(x)| auf Differenzierbarkeit in x_0 = 0
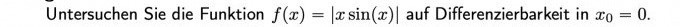
Wolphram Alpha sagt bescheid dass die Funktion nicht auf ganz R differzierbar ist. (EDIT: korrigiert gemäss Abbildung im Kommentar).
Aber nach meiner Rechnungen ist der Limes der Differenzenquotient für h->0- und h->0+ gleich und bestimmt.
Vielen Dank im Voraus!