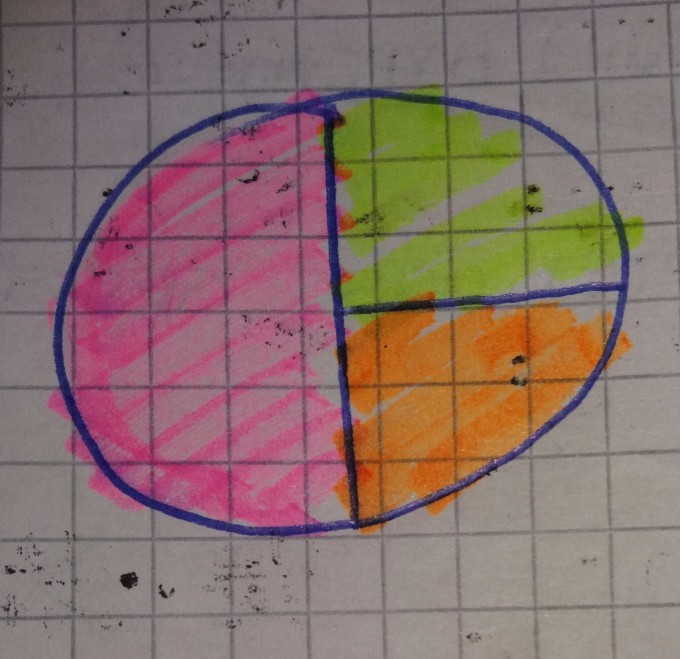
 Aufgabe:
Aufgabe:
Bei einer Lotterie zahlt man den Einsatz von 50cent und dreht das Glücksrad zweimal. Bei zwei gleichen Farben wird ein Euro ausbezahlt sonst nichts.
a) Gib die Wahrscheinlichkeitsverteilung der Zufallsvariablen "Gewinn in Euro" an
b) Kann man den Einsatz so ändern, dass die Lotterie fair ist ?
Problem/Ansatz:
Hab wirklich KP wie man es berechnet, wäre froh wenn jemand mir erklären könnte !