Aufgabe:
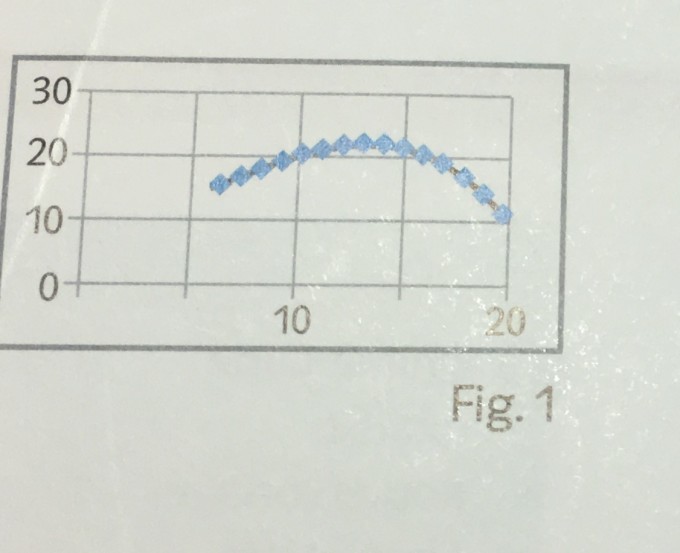
Die Funktion f mit f(x)= 0,01x^3 +0,2x^2 +10 beschreibt für x∈ (6;20) nährungsweise die Temperatur in Grad Celsius von 6 Uhr bis 20 Uhr im Laufe eines Tages (Fig. 1)
a) Berechnen Sie Temperaturänderung um 10 Uhr uns um 20 Uhr.
b) Berechnen Sie die durchschnittliche Temperaturänderung in den ersten vier Stunden seit Beobachtungsbeginn .
c) Berechnen Sie die momentane Temperaturänderung um 10 Uhr morgens .
d) Berechnen Sie die Uhrzeit , zu der die Funktion die höchste Temperatur liefert .
Problem/Ansatz:
Ich wollte fragen, ob meine Ergebnisse richtig sind ?