Bestimmen von quadratischer Funktion, die die Funktion f(x)= x^3-6x^2+9x+1 im Hochpunkt berührt und

Question

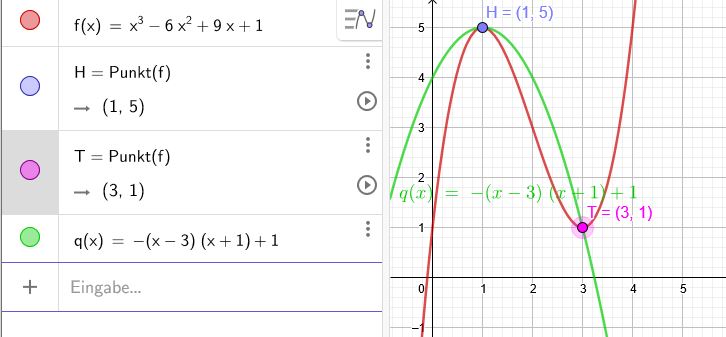
Aufgabe: Gib eine quadratische Funktion an, die die Funktion f(x)= x^3-6x^2+9x+1 im Hochpunkt berührt und im Tiefpunkt (nur) schneidet.

Answer 1

Hallo

 1. bestimme den Hochpunkt (xh,yh) und Tiefpunkt (xt,yt) von f(x)

2. die Parabel y=ax^2+b*x+c

 und du weisst: y(xh)=yh, y'(xh)=0 y(xt)=yt

 also hast du 3 Gleichungen für a,b,c

Gruß lul

Answer 2

Skizze mit Ansatz einer Parabelgleichung in Scheitelpunktform y = 5 - a(x-1)^2

~plot~ x^3-6x^2+9x+1;5-(x-1)^2;5-2(x-1)^2;5-0,5(x-1)^2 ~plot~