Polarform berechnen von z= √3 +i

Question

Aufgabe:

z= √3 +i

Problem/Ansatz:

Stellen die komplexen Zahlen in Polarform

Vielen Dank für die Hilfe !

Answer 1

Polarform :

z= r (cos(a) +i sin(a))

r= √(3+1)=2

tan a= Imaginärteil/Realteil =1/ √3 = √3/3

a= 30°

->

z= 2 (cos(30°) +i sin(30°)

Answer 2

Wie schon zuvor. Es ist \(\Re(z)=\sqrt{3}\) und \(\Im(z)=1\). Der Betrag ist \(|z|=r=\sqrt{(\sqrt{3})^2+1^2}=2\). Wieder in der gaußschen Zahlenebne dargestellt:

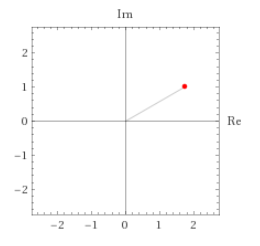
Der Winkel \(\varphi\) berechnet sich aus dem Arkustangens von \( \frac{1}{\sqrt{3}}\). Die Polarform ist \(z=r\cdot e^{i\cdot \varphi}\)