Hallo vika,
Du hast nicht näher beschrieben, was für Koordinaten der Vektor \(AB\) hat. In jedem Fall reicht es aus, den Vetktor so zu verschieben (nur verschieben, nicht drehen!), so dass der Anfang des Vektors (bei \(A\)) mit dem Punkt \(C=(1|\,4)\) zusammen fällt.
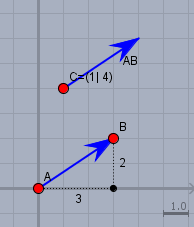
Mal angenommen, \(AB\) hat die Koordinaten \(AB=(3|\,2)\). Dann verschiebt man den Vektor wie oben in der Skizze und liest die Koordinaten der neuen Spitze ab. In diesem Fall ist das $$\quad \dots = \begin{pmatrix} 4 \\ 6\end{pmatrix}$$das kann man auch ausrechnen, indem man zu den Koordinaten von \(C\) die von \(AB\) einfach hinzu addiert - die Position der neuen Spitze berechnet sich aus$$\quad \dots = \begin{pmatrix} 1 \\ 4\end{pmatrix} + \begin{pmatrix} 3 \\ 2\end{pmatrix} = \begin{pmatrix} 1+3 \\ 4 + 2\end{pmatrix} = \begin{pmatrix} 4 \\ 6\end{pmatrix}$$ Falls noch etwas unklar ist, so frage bitte nach.
Gruß Werner