Aufgabe:
Für die Zwecke unserer Diskussion gehen wir von einem Alter bei Pensionierung von 67 Jahren aus. Angenommen, Sie beginnen mit Null Dollar, in Ihrem Alter**, heute, und Sie beginnen, 500 Dollar pro Monat, jeden Monat, von der Gegenwart bis zum Alter von 67 Jahren, zur Seite zu legen. Wie viel Geld werden Sie zur Verfügung gestellt haben?
Nehmen wir an, dass Ihre Ersparnisse mit einer jährlichen Rendite von 7% angelegt werden. Wie viel Geld wirst du im Alter von 67 Jahren haben? Würde es einen Unterschied machen, wenn Sie jeden Monat zusätzliche $100 für insgesamt $600 investieren würden?
Ursprünglische Aufgabe:
For purposes of our discussion, we assume an age at retirement of 67. Assuming that you start with zero dollars, at your age**, today, and you begin setting aside $500 per month, each month, from the present until age 67. How much money will you have set aside?
Now, assume that your savings are invested at a annual return rate of 7%. How much money will you have at age 67? Would it make a difference if you invested an additional $100 each month, for a total of $600?
Problem/Ansatz:
Guten Tag Leute,
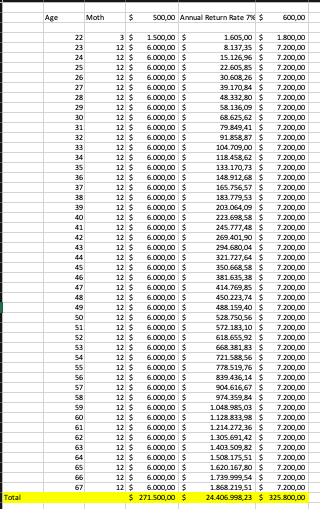
meint Ihr ich habe die Aufgabe richtig verstanden und gelöst? Ich habe eine Exceltabelle benutzt, weil es damit schneller und einfacher ging. Ich würde mich über jeden verbesserungsvorschag freuen.
(Das erste Jahr hat nur 3 Monte, da 2019 nur noch Oktober, November und Dezember hat.)
Vielen Dank im voraus für eure Hilfe.
Gruß