Schnittpunkt berechnen

Question

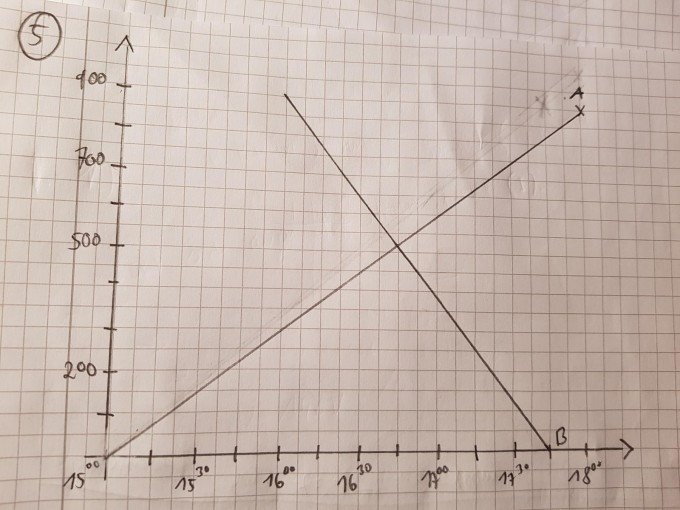
Ein Bergsteiger verlässt um 15:00 Uhr den Parkplatz und steigt mit konstanter Geschwindigkeit zur 900m höher gelegenen Hütte auf, die er um 18:00 Uhr erreicht. Um 16:00 verlässt ein anderer Bergsteiger die Hütte und erreicht den Parkplatz um 17:45 Uhr.

a) Um wieviel Uhr treffen sich die beiden Bergsteiger?

b) Wie hoch sind sie dann über dem Parkplatz?

Ich habe zuerst ein Koordinatensystem (nach Maßstab aus der Aufgabe) aufgestellt, dann für jeden Bergsteiger eine Gerade eingezeichnet und versucht den Schnittpunkt beider zu bestimmen. Nur irgendwie komme ich mit meinem Ergebnis nicht hin.

Für Bergsteiger A habe ich die Punkte P1(15|0) P2(18|900) und

Für Bergsteiger B die Punkte (16|900) und (17,45|0) genommen.

Laut Lösung treffen sich die beiden um  16:44 Uhr und sind 520m über dem Parkplatz.

Mein Schnittpunkt: S(16,652 | 495,6)

Answer 1

Das sieht rechnerisch so aus:

900/3·(x - 15) = (- 900/1.75)·(x - 16) + 900 --> x = 318/19 = 16.74 = 16:44 Uhr

900/3·(318/19 - 15) = 9900/19 = 521.1 m

Comments

Danke für die Antwort

Aber wieso klappt meine Lösung nicht?

Ich habe für Bergsteiger A die Gerade y₁=300x - 4500

Und für Bergsteiger B y₂=-620,68x + 10831,03

Bin ich die Aufgabe falsch angegangen? Also ist mein Lösungsansatz generell falsch?

---

Die Funktion für Bergsteiger 2 stimmt bei dir nicht. Die von Bergsteiger 1 stimmt.

Korrekt wäre

y = 63900/7 - 3600/7·x

oder Näherungsweise

y = 9129 - 514.3·x

---

Hab mir schon fast gedacht, dass da irgendwas nicht stimmen kann..

Hmm... Aber wieso? Hab das alles schon nachgerechnet. -.- Dann müssen meine Punkte für Bergsteiger B falsch sein (?)

Für B:

m = 0-900 / 17,45-16 =  -900/1,45 = -620,69

y = -620,69x + b

P2 eingesetzt:

0 = -620,69*17,45 + b

0 = -10831,03 + b |+ 10831,03

10831,03 = b

ergibt: y = -620,69x + 10831,03

---

Wo ist der Fehler bei meiner Lösung???

---

17:45 ≠ 17.45

17:45 = 17.75 !!

---

Argh nein..... Ich depp...

Dankesehr!