Aufgabe:
Gegeben ist die Funktion f mit f(x)= 7/16x^2+2
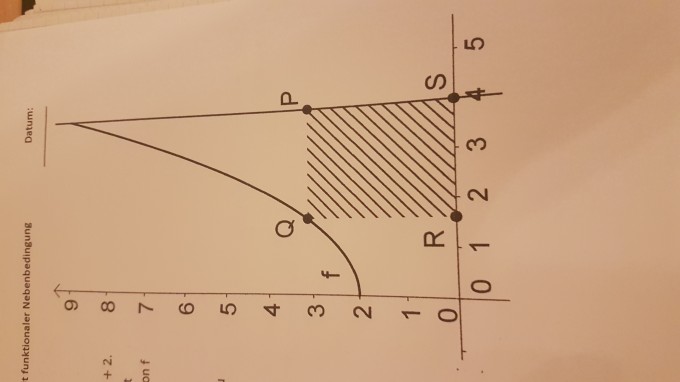
Eine senkrechte Gerade bei x=4 begrenzt mit den Koordinatenachsen und dem Graphen von f eine Fläche , in der ein Rechteck liegen soll, dessen Seiten auf oder parallel zu den Koordinatenachsen ist.
Wie ist der Punkt Q auf dem Graphen von f zu wählen , damit das Rechteck maximalen Flächeninhalt hat ?
Problem/Ansatz:
Moin , da ich lange gefehlt habe , habe ich große Probleme die Aufgabe zu lösen , ich bitte um Hilfe.
LG