Fläche unter einem Kreisabschnitt berechnen

Question

Anhand eines praktischen Beispiels möchte ich mein Problem darstellen.

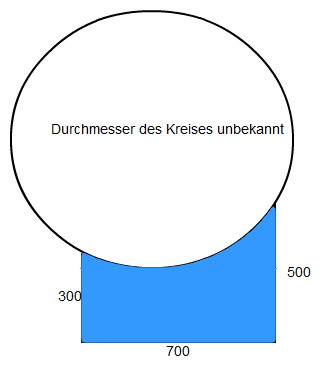
Ich möchte die unten abgebildete blaue Fläche berechnen. Die Zeichnung ist etwas ungenau.

Es soll eine Fläche unter einem Kreisabschnitt darstellen.

Zur Erklärung: Die Maße sind in der Praxis variabel, der Kreis an den die Fläche angrenzt ist im Durchmesser auch variabel. Und die Lage auf dem Kreis ist auch variabel.

Wie schaffe ich es diese Fläche zu berechnen?

Habe von Integralrechnung keinen blassen Schimmer und stoße hier an meine Grenzen.

.

 

Answer 1

Das ist so nicht möglich, weil es durch diverse Kreisradien unendlich viele Lösungen gibt. Ich habe das mal für deine Skizze aufgezeichnet.

Ich habe hier nur mal 2 aus unendlichen vielen Möglichkeiten herausgepickt.

Comments

Wäre eine Lösung denkbar wenn der Durchmesser bekannt wäre?

---

Ja. Dann wäre eine Lösung denkbar

Dann ist das ganze ja eindeutig.

---

Kannst Du mir bitte einen Lösungsweg aufzeigen für einen definierten Durchmesser in dem spezifischen Problem?

---

Du kannst den Abstand der beiden Punkte berechnen durch die der Kreis geht.

s = √(7^2 + 2^2) = √53

Du brauchst also Trapezfläche minus dem Kreisabschnitt

Die Trapezfläche sollte hier recht einfach sein. 

A = 1/2 * ( 3+ 5) * 7

Der Kreisabschnitt ist schon anspruchsvoller. Dafür habe ich mal eine Formel von 

https://de.wikipedia.org/wiki/Kreissegment

zusammengebastelt. Dort kommt nur noch das s und das r drin vor. Ich hoffe das kommt so hin. Zu testen wäre das an ein paar Beispielen.

Kreisabschnitt: A = r^2·ASIN(s/(2·r)) - s·√(4·r^2 - s^2)/4