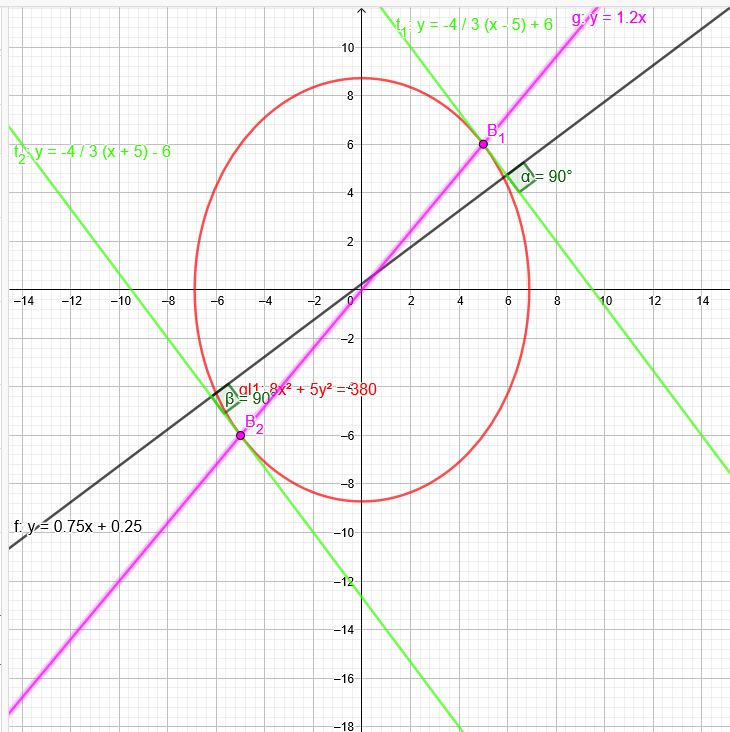
Tangentengleichungen an Ellipse ermitteln, die normal zu Geraden g sind
e:\(8x^2+5y^2=380\)
\(g:y=0,75x+0,25\) \(m_g=0,75\)→ \(m_n=-\frac{4}{3}\)
\(f(x,y)=8x^2+5y^2-380\)
\(f_x(x,y)=16x\)
\(f_y(x,y)=10y\)
\(f'(x)=-\frac{f_x(x,y)}{f_y(x,y)}\)
\(f'(x)=-\frac{16x}{10y}=\frac{1,6x}{y}\)
\(m_n=-\frac{4}{3}\)
\(-\frac{4}{3}=-\frac{1,6x}{y}\)
\(\frac{1}{3}=\frac{0,4x}{y}\)
\(y=1,2x\)
Diese Gerade schneidet die Ellipse in den Berührpunkten:
\(8x^2+7,2x^2=380\)
\(x_1=5\) \(y_1=6\)
\(x_2=-5\) \(y_2=-6\)
1.Tangente:
\( \frac{y-6}{x-5}=-\frac{4}{3} \)
\( y=-\frac{4}{3}(x-5)+6 \)
2.Tangente:
\( \frac{y+6}{x+5}=-\frac{4}{3} \)
\( y=-\frac{4}{3}(x+5)-6 \)