Die Methode der Intervallhalbierung: f(x) = 2(x+3/2)(x+3)(x-3/2), a0=-4.5, b0= 4.5

Question

\( f(x)=2\left(x+\frac{3}{2}\right)(x+3)\left(x-\frac{3}{2}\right), x \in \boldsymbol{R} \)

Entscheide welche der Nullstellen von \( f \) Grenzwert der Folgen \( \left(a_{n}\right) \) und \( \left(b_{n}\right) \) ist falls:

1. \( a_{0}=\frac{-9}{2}, b_{0}=\frac{9}{2} \)
2. \( a_{0}=0, b_{0}=\frac{5}{2} \)
3. \( a_{0}=\frac{-7}{2}, b_{0}=5 \)

Ich weiß, wie man Methode der Bisektion anwendet nur weiß ich nicht, wie man den grenzwert errechnet. Ich meine soll ich so lange rechnen mit dieser Methode bis ich einen genauen Wert habe?

Comments

Vermutlich musst du einfach mal ein paar Werte berechnen.

Also f(a0) , f(b0) ausrechnen. Falls Vorzeichen unterschiedllich:

f(Mitte) betrachten und entscheiden, ob Mitte zu a1 oder b1 wird.

Du darfst danach bestimmt auch mit der Skizze deiner Funktion argumentieren.

---

Das weiß ich ja, nur muss ich den Grenzwert in das Applet eingeben, d.h. keine Skizze oder ähnliches. Und Soll ich dass dann solange rechnen bis ich denke "ja, der Wert springt zwischen den beiden Zahlen, also muss dies der Grenzwert sein?"

---

Und Soll ich dass dann solange rechnen bis ich denke "ja, der Wert springt zwischen den beiden Zahlen, also muss dies der Grenzwert sein?"

Ja genau. Wenn Konvergenz sollte eine der drei Nullstellen rauskommen.

---

Ok ich versuchs mal C:

---

Leider komm ich auf gar keinen vernünftigen Grenzwert. Mal ist der Wert eine Zeit lang positiv, dann wieder Negativ. Irgendwelche anderen Tipps?

---

Du musst systematisch zwischen pos. und neg. Funktionswerten weitersuchen. Das macht der Bisektionsalgorithmus.

Answer 1

Die Methode der Intervallhalbierung: f(x) = 2(x+3/2)(x+3)(x-3/2),

Skizze (mit Faktor 10 gestaucht in y-Richtung. D.h. y-Achsenschnittpunkt bei -13.5

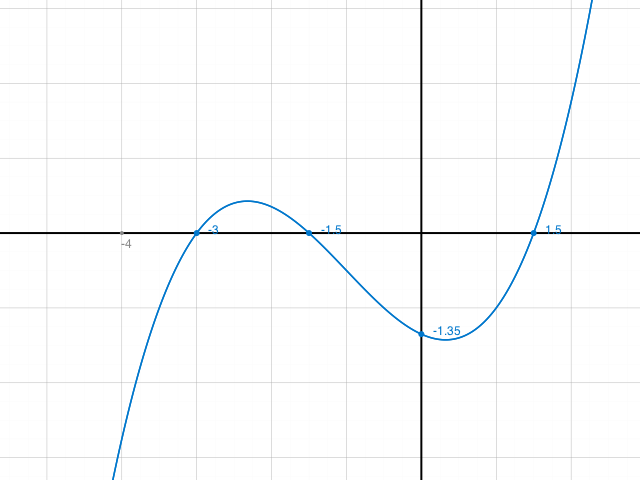
Nullstellen -3, -1.5, 1.5

f(x) < 0 für x < -3 und für -1,5 <x<1.5

f(x) > 0 für -3 < x < -1.5 und für 1.5<x

Diese Aufstellung wird in der Folge benutzt.

a0=-4.5, b0= 4.5, 

f(a0) < 0, f(b0) > 0, f(0) < 0. 

Daher 

a1 = 0, b1 = 4.5, eigentlich ist hier schon klar, dass man bei x=1.5 landet.

f(a1) < 0, f(b1)> 0, f(2.25) > 0

a2 = 0, b2 = 2.25, Mitte 1.125 

f(a2) <0, f(b2) > 0, f(1.125) <0

a3=1.125, b3=2.25 usw.

konvergiert gegen 1.5.
 

Comments

Woher kommste drauf dass es gegen 1,5 konvergiert?

---

Ich konvergiere gegen 1,5 wenn ich für a0=0 und b0= 2,5 setze


Und bei 3. erhalte ich für a1= 0,75 und b1=5 Konvergiert dieser wert dann nicht auch zu 1,5?

---

Doch. Bei den beiden kommt ebenfalls 1.5 raus.

---

Also konvergieren alle 3 gegen 1,5. Scheint mir komisch aber wenn man erstmal mit den zahlen spielt führt kein weg drumherum, Danke vielmals Lu (:

---

Jetzt kannst du dir noch überlegen, wie genau du die Nullstellen kennen musst, um mit  einem andern Anfangsintervall via Bisektionsverfahren die andern Nullstellen auch noch zu finden.

Es reicht bei Polynomen 3. Grades, wenn man eine Nullstelle findet, dann kann man via Polynomdivision das Problem auf eine quadratische Gleichung reduzieren. Da gibt's dann eine Formel und man hat dann sicher alle Nullstellen ;)

---

Heute haben wir differenzierbarkeit behandelt und partialbruchzerlegung und polynomdivision. Muss erst mal diese Sachen lernen und die Aufgabendazu erledigen. Danke trotzdem Lu (: