Integral bestimmen (Flächeninhalt)

Question

Aufgabe

Folgendes Integral von f(t) = -2t bestimmen.

2 ist obere Grenze

-1 ist untere Grenze

\( \int\limits_{-1}^{2} \)  -2t dt

Bestimmen sie das Integral mithilfe von Dreiecks und Rechtecksflächen.

Problem/Ansatz:

Ich habe keine Ahnung wie das gehen soll.

Answer 1

Integral

2 = Obersumme

-1 = Untersumme

Bitte zeichnen. Ist das eine Antwort, eine Frage oder was?

Text erkannt:

\( \int \limits_{0}^{\infty} \)-2 t  d t 
Bestimmen sie das Integral mithilfe von Dreiecks und Rechtecksflächen.

Dieses Integral existiert nicht. Weder mit Dreiecks- noch mit Rechtecksflächen.

Comments

Sorry ich wusste nicht genau wie das hier mit dem zeichnen funktioniert. Also die Obersumme 2 ersetzt in dem Fall das Unendlich Zeichen und die Untersumme -1 steht am unteren Rand des Integrals und ersetzt die 0.

Danke trotzdem :)

---

Habe nun mal die Fragestellung berichtigt.

Das Minus vor 2t im Integranden stimmt?

---

Der Plotter zeichnet nur wenn man  die Variable auf der horizontalen Achse x nennt.

~plot~ x = -1; x=2;-2x ~plot~

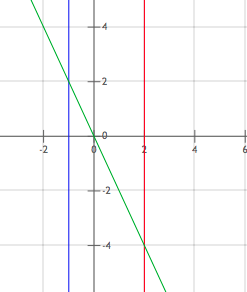
Hier siehst du 2 Dreiecke.

Links der y-Achse ( und oberhalb der x-Achse) Fläche 1*2 / 2 = 1

Rechts der y-Achse ( und unterhalb der x-Achse) Fläche 2*4 / 2 = 4

Somit gilt

Gesuchtes Integral = 1 + (-4) = -3 

Answer 2

Das gesuchte Integral ist die blaue Fläche minus die grüne Fläche. Da beides rechtwinklige Dreiecke sind, musst du die Formel für den Flächeninhalt eines Dreiecks verwenden. Du kannst die Dreiecke auch als halbe Rechtecke ansehen.

Das blaue Dreieck hat einen Flächeninhalt von 1, das grüne einen Inhalt von 4. Also ist das Integral 1-4=-3.

Answer 3

∫ (-1 bis 2) (-2 * t) dt = 1/2 * 1 * 2 - 1/2 * 2 * 4 = 1 - 4 = -3