Hallo,
wenn Du wissen möchtest, ob Dein Ergebnis richtig ist, so kannst Du auch eine Zeichnung anfertigen und den Winkel nachmessen:
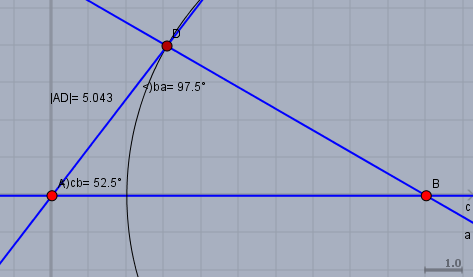
Man kann ablesen, dass \(\alpha \approx 52,5°\) und \(\gamma \approx 97.5°\) ist.
Um den Sinussatz anzuwenden, benötigst Du jeweils zwei Paar aus einem Winkel und einer gegenüberliegenden Seite, von denen drei Größen bekannt sein müssen. Das ist hier aber nicht der Fall, da die Seite \(b\), die dem einzigen bekannten Winkel \(\beta\) gegenüberliegt, nicht bekannt ist. Berechne man also zunächst \(b\) mit dem Kosinussatz $$\begin{aligned} b^2 &= a^2 + b^2 - 2ab\cos \beta \\ &= 8^2 + 10^2 - 2 \cdot 8 \cdot 10 \cos 30° \\ &= 164 - 160 \cdot \frac 12 \sqrt 3 \\ &= 164 - 80 \sqrt 3\\ \implies b &= \sqrt{164 - 80 \sqrt 3} \approx 5,043 \end{aligned}$$Und nun zum Sinussatz:$$\begin{aligned} \frac{\sin \alpha}{a} &= \frac {\sin \beta}{b} \\ \implies \sin \alpha &= a \cdot \frac {\sin \beta}{b} \\ &= 8 \cdot \frac{\sin 30°}{5,043} \\&\approx 0,7931 \\ \implies \alpha &\approx \arcsin(0,7931) \approx 52,48° \end{aligned}$$