Bestimme den punkt s so dasss es in der ebene liegt

Question

Aufgabe:

Eine gerade quadratische pyramide hat die Grundenkantenlänge 5 m und die höhe 10 m. Die Grundläche liegt in der xy ebene. Die punkte A, B , C und D liegen auf den Seitenkanten . Der punkt A in einer Höhe von 4 m , die Punkte B und C in einer Höhe von 6  m . Die Ebene E enthält die Punkte A, B und C . Bestimme die Koordinaten des punktes D so das es in der ebene E liegt

Answer 1

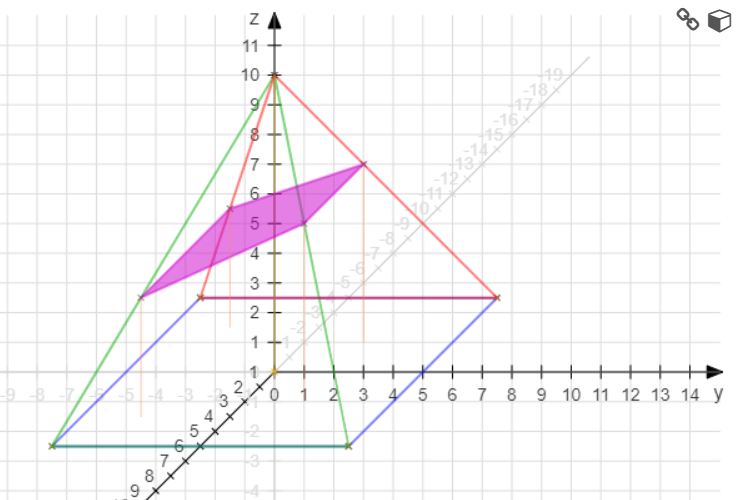
Da hier weder Zeichnung noch nähere Angaben gegeben sind ist das Beantworten höchst spekulativ. Ich denke mir also einfach Gegebenheiten aus:

A = [5, -5, 0] + r [-5, 5, 10] = [x, y, 4] → x = 3 ∧ y = -3 ∧ r = 0.4 → A = [3, -3, 4]
B = [5, 5, 0] + r [-5, -5, 10] = [x, y, 6] → x = 2 ∧ y = 2 ∧ r = 0.6 → B = [2, 2, 6]
C = [-2, 2, 6]
D = [-3, -3, 4]

Bei mir hätte D die Koordinaten D(-3, -3, 4)

Comments

Deine Kantenlänge ist 10m und nicht 5m

---

Stimmt. Danke für die Verbesserung ullim

D.h. die x und y-Koordinaten sind einfach nur durch 2 zu teilen.

Ich denke das bekommt der Fragesteller auch noch selber hin.

Answer 2

\(\vec{OD} = \vec{OC} + \vec{BA}\)

Comments

Wie bestimmt man die punkte . Könnten sie die lösung schreiben und ich überprüfe es mit meiner lösung.

---

Wie bestimmt man die punkte

Die Punkte können nicht bestimmt werden, weil die Lage der Grundfläche in der xy-Ebene nicht bekannt ist.

Die Spitze der Pyramide hat den Ortsvektor

\( \vec{OS} = \vec{OM} + \begin{pmatrix} 0\\0\\10 \end{pmatrix} \)

wobei \(M\) der Höhenfusspunkt der Pyramide ist. Den berecnest du mittels

\( \vec{OM} = \frac{1}{2}\left(\vec{OP}+\vec{OR}\right) \)

wobei \(P\) und \(R\) gegenüberliegende Ecken der Grundfläche sind.

Könnten sie die lösung schreiben und ich überprüfe es mit meiner lösung.

Umgekehrt wäre mir lieber, du bestimmst die Punkte und ich überprüfe, ob die richtig sind.