Aufgabe:
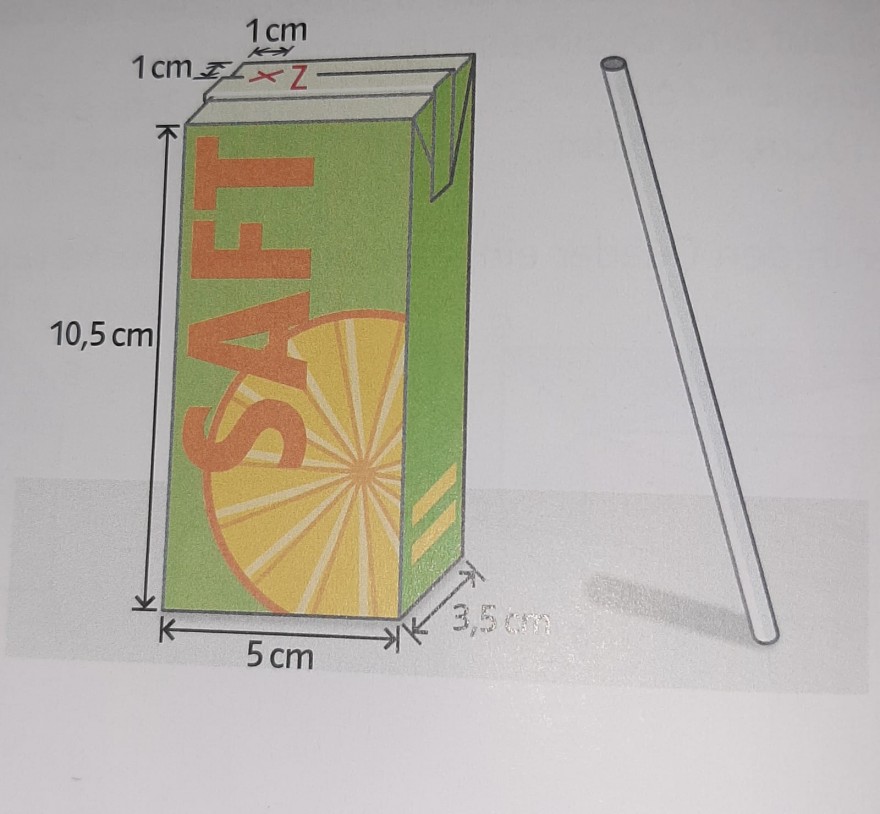
Aus einem quaderförmigen Trinkbehälter soll mit einem Strohhalm, wekcher durch den Punkt Z verläuft, getrunken werden. Wie lang muss dieser mindestens sein, damit er nicht im Trinkbehälter verschwindet?
Problem/Ansatz:
Ich habe meinen Ergebnis im Anhang eingefügt, ist es richtig?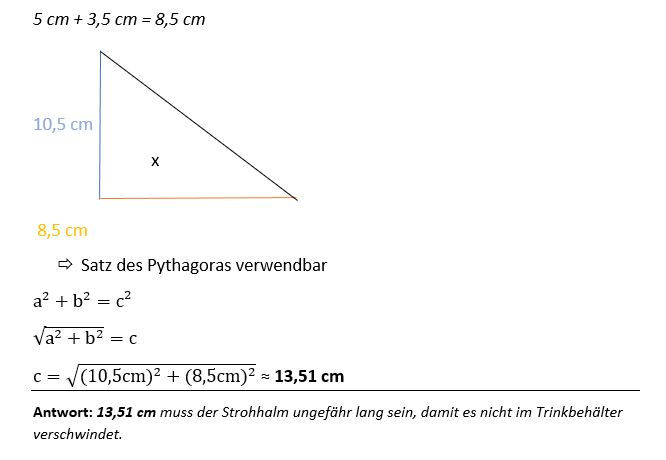
Text erkannt:
\( 5 \mathrm{cm}+3,5 \mathrm{cm}=8,5 \mathrm{cm} \)
\( 10,5 \mathrm{cm} \)
\( x \)
\( 8,5 \mathrm{cm} \)
\( \Rightarrow \) Satz des Pythagoras verwendbar
\( a^{2}+b^{2}=c^{2} \)
$$ \sqrt{a^{2}+b^{2}}=c $$
\( c=\sqrt{(10,5 \mathrm{cm})^{2}+(8,5 \mathrm{cm})^{2}} \approx 13,51 \mathrm{cm} \)
Antwort: \( 13,51 \mathrm{cm} \) muss der Strohhalm ungefähr lang sein, damit es nicht im Trinkbehälter verschwindet
Text erkannt:
11