Welche Gemeinsamkeit weisen die beiden Vektoren auf?

Question

Aufgabe:Man soll begründen mithilfe einer Zeichnung , dass der Vektor a= (1,-2) nicht gleich dem Vektor b= (-1,2) ist.

Welche Gemeinsamkeit weisen die beiden Vektoren auf?

Answer 1

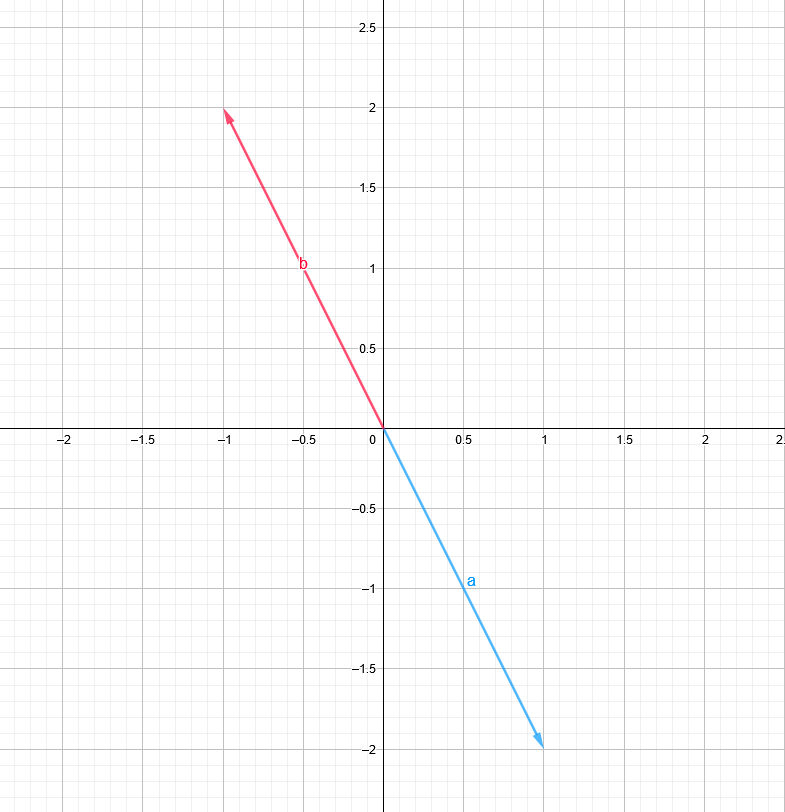
Hallo,

beide haben die gleiche Länge, sind aber genau entgegengesetzt orientiert, man spricht vom Gegenvektor. Es gilt nämlich, dass \(\vec{a}=-\vec{b}\).

Sprechweise: \(\vec{a}\) ist der Gegenvektor von \(\vec{b}\) bzw. \(\vec{b}\) ist der Gegenvektor von \(\vec{a}\).

Jeweils einen Repräsentanten von \(\vec{a}\) und \(\vec{b}\) habe ich hier zeichnen lassen:

Answer 2

Zeichne beide Vektoren als Ortsvektoren (also beginnend bei (0|0)). Dann endet Vektor(1,-2) in Punkt  (1,-2) und Vektor(-1,2) im Punkt (-1,2).

Answer 3

Beide Vektoren haben den gleichen Betrag und gleiche Richtung, aber unterschiedliche Orientierung.