Hallo Svenja,
wenn die Geraden \(g\) und \(h\) orthogonal zu einander verlaufen, dann muss das Skalarprodukt ihrer Richtungsvektoren \(=0\) ergeben.$$\begin{pmatrix}4\\ 2\\ -1\end{pmatrix} \cdot \begin{pmatrix}5\\ -7\\ 5\end{pmatrix} = 20 - 14 - 5 = 1 \ne 0$$sie sind also nicht senkrecht zu einander.
Wenn \(g\) und \(h\) sich schneiden, so muss folgende Gleichung$$\begin{aligned} g(r) &= h(s) \\ \begin{pmatrix}3\\ 0\\ 1\end{pmatrix} + r \cdot \begin{pmatrix}4\\ 2\\ -1\end{pmatrix} &= \begin{pmatrix}3\\ 1\\ 4\end{pmatrix} + s \cdot \begin{pmatrix}5\\ -7\\ 5\end{pmatrix}, \quad r,s \in \mathbb{R}\end{aligned}$$eine Lösung haben. Dazu berechnet man \(r\) und \(s\) aus zwei der drei Koordinatengleichungen$$\begin{aligned}3 + 4r &= 3 + 5s \\ 2r &= 1 - 7s \\ \implies r &= \frac 5{38}, \quad s = \frac 4{38}\end{aligned}$$Setzt Du diese Lösung in die dritte Koordinatengleichung ein$$ 1 - \frac 5{38} \ne 4 + 5 \cdot \frac 4{38}$$so geht dies nicht auf. Die Geraden schneiden sich also nicht. wie auch hier zu sehen ist:
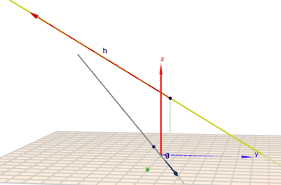
(klick auf das Bild)