Für welche p, q ∈ Z ist die Funktion f_(pq) stetig in 0

Question

Die Funktion zack : R → R sei die Funktion mit der Eigenschaft zack(x) = |x| für |x|≤ 1/2 und zack(x+n) = zack(x) für x∈R und n∈N.

Für p, q ∈ Z definieren wir die Funktion f_pq : R → R durch

\( f_{p q}(x):=\left\{\begin{array}{ll}|x|^{p} \operatorname{zack}\left(|x|^{q}\right), & \text { falls } x \neq 0 \\ 0, & \text { falls } x=0\end{array}\right. \)

Ich soll bestimmen, für welche p, q ∈ Z die Funktion f_pq stetig in 0 ist.

Answer 1

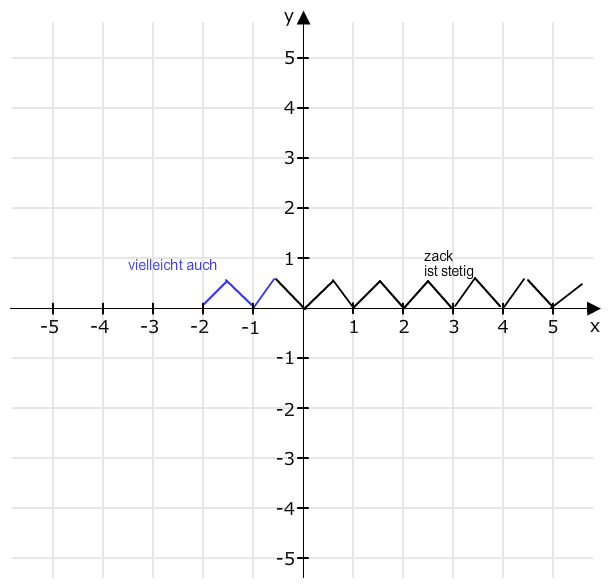
Die Funktion zack : R → R sei die Funktion mit der Eigenschaft zack(x) = |x| für |x|≤ 1/2 und zack(x+n) = zack(x) für x∈R und n∈N.

Erst mal die Funktion zack. Die beginnt nach Definition mit einem Zacken |x|. und dann weiter mit den gleichen Zacken. Mindestens Richtung rechts. Ob man das auch Richtung links so lesen kann, ist mir unklar. In der Fortsetzung scheint es so, da x aus R kommt. 

Als Erstes kann man mal feststellen, dass zack stetig und beschränkt ist, wo zack definiert ist. 

 

Für p, q ∈ Z definieren wir die Funktion f_pq : R → R durch 

.....

 

In der Behauptung hat zack keine negativen Argumente wegen der Betragsfunktion. f_pq ist symmetrisch zu x=0.

Zudem interessiert man sich nur für die Stelle 0. Also Grenzwerte für x von links und von rechts gegen 0.

ohne Einschränkung der Allgemeinheit, kann man annehmen, dass x> 0.

Da x gegen 0 geht, kann man voraussetzen, dass 0<x<0.5

x^p * x^q =  x^pq       

x^pq geht für x gegen 0 gegen 0, wenn qp>0. Daher stetig in 0, falls pq>0.

Für pq=0 wäre der Grenzwert von rechts 1

und für pq<0 wäre er +∞, d.h. er ex. gar nicht. in den beiden letzten Fällen ist f_pq nicht stetig in 0.

Also f_pq (x) stetig in x=0 gdw pq>0.