Kreiskonstruktion k2 - welcher k1 von innen in A berührt sowie durch B verläuft

Question

Ein Kreis k1 mit Mittelpunkt M1, einem Punkt A auf der Kreislinie und einem Punkt B im Inneren des Kreises sind gegeben. B ist nicht M1 und die Punkte sind nicht kollinear.

Ich soll eine Ausgangssituation für den Kreis und die Punkte konstruieren und dann nur mir Zirkel und Lineal k2 mit M2 konstruieren, welcher k1 von innen in A berührt sowie durch B verläuft.

Ich hätte jetzt gedacht M1, A und B bilden ein Dreieck und k2 ist der Umkreis von dem Dreieck. Aber A soll ja nur berührt werden, oder wie ist das gemeint?
So wäre meine konstruierte Ausgangssituation:

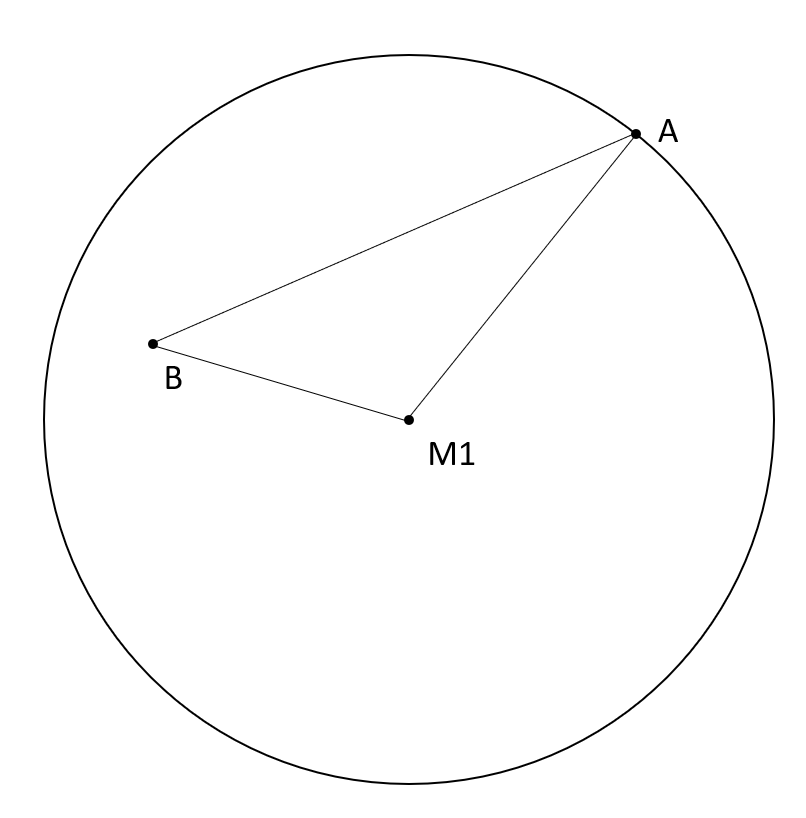
Text erkannt:

8

Answer 1

Hallo,

die Mittelpunkte aller Kreise, die \(k_1\) in \(A\) berühren, liegen auf der Geraden (rot) durch \(A\) und \(M_1\).

Und die Mittelpunkte aller Kreise, die \(A\) und \(B\) enthalten, liegen auf der Mittelsenkrechten (blau) der Strecke \(AB\). Folglich ist \(M_2\) der Schnittpunkt dieser beiden Geraden.

Ziehe eine Gerade durch \(A\) und \(M_1\) und konstruiere die Mittelsenkrechte über \(AB\). Der Schnittpunkt ist \(M_2\).

Answer 2

Verlängere AM1 zum Durchmesser.

Zeichne bei B einen rechten Winkel ein. (Thales lässt grüßen.)

Der Schnittpunkt der gerade gezeichneten Linien sei C.

Konstruiere den Mittelpunkt der Streck AC. Er ist der Mittelpunkt M2 des gesuchten Kreises durch A, B und C.

:-)